题目内容
 如图,已知Rt△AOB的锐角顶点A在反比例函数y=
如图,已知Rt△AOB的锐角顶点A在反比例函数y=| m |
| x |
(1)求反比例函数的解析式;
(2)一条直线过A点且交x轴于C点,已知tan∠ACB=
| 2 |
| 7 |
分析:(1)由△AOB的面积为3和OB=3可得AB=2,即A(3,2),将A(3,2)代入到y=
中,可得m=6,即y=
.
(2)由tan∠ACB=
得
=
得BC=7又OB=3,则OC=4,即C(-4,O),而A(3,2),故可得AC的解析式为:y=
x+
.
| m |
| x |
| 6 |
| x |
(2)由tan∠ACB=
| AB |
| BC |
| 2 |
| 7 |
| AB |
| BC |
| 8 |
| 7 |
| 8 |
| 7 |
解答:解:(1)∵△AOB为Rt△
∴S△AOB=
OB•AB
∴3=
•3•AB
∴AB=2
∴A(3,2)(2分)
A在反比例函数的图象上
∴将A(3,2)代入到y=
中
2=
m=6
∴y=
.(5分)
(2)在Rt△ABC中
tan∠ACB=
∴
=
∵AB=2,
∴BC=7
又∵OB=3
∴OC=4
∴C(-4,O)(7分)
∴A(3,2),C(-4,O)
∴设AC的解析式为y=kx+b(k,≠0)
∴
∴
(9分)
∴AC的解析式为:y=
x+
(10分)
∴S△AOB=
| 1 |
| 2 |
∴3=
| 1 |
| 2 |
∴AB=2
∴A(3,2)(2分)
A在反比例函数的图象上
∴将A(3,2)代入到y=
| m |
| x |
2=
| m |
| 3 |
m=6
∴y=
| 6 |
| x |
(2)在Rt△ABC中

tan∠ACB=
| AB |
| BC |
∴
| 2 |
| 7 |
| AB |
| BC |
∵AB=2,
∴BC=7
又∵OB=3
∴OC=4
∴C(-4,O)(7分)
∴A(3,2),C(-4,O)
∴设AC的解析式为y=kx+b(k,≠0)
∴
|
∴
|
∴AC的解析式为:y=
| 2 |
| 7 |
| 8 |
| 7 |
点评:本题考查反比例函数和一次函数解析式的确定、图形的面积求法等知识及综合应用知识、解决问题的能力.有点难度.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 如图,已知Rt△ABC外切于⊙O,E、F、H为切点,∠ABC=90°,直线FE、CB相交于D点,连接AO、HE、HF,则下列结论:①∠EFH=45°;②∠FEH=45°+∠FAO;③BD=AF;④DH2=AO•DF.其中正确结论的个数为( )
如图,已知Rt△ABC外切于⊙O,E、F、H为切点,∠ABC=90°,直线FE、CB相交于D点,连接AO、HE、HF,则下列结论:①∠EFH=45°;②∠FEH=45°+∠FAO;③BD=AF;④DH2=AO•DF.其中正确结论的个数为( )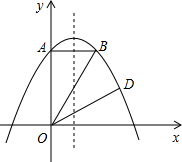 梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由. 梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由. ,
, ).
). ,
, ).
).
