题目内容
1.已知实数m,n满足m-n2=1,则代数式m2+2n2+6m+8的最小值等于15.分析 把m-n2=1变形为n2=m-1,代入所求式子,根据配方法进行变形,根据偶次方的非负性解答即可.
解答 解:∵m-n2=1,
∴n2=m-1,m≥1,
∴m2+2n2+6m+8
=m2+2m-2+6m+8
=m2+8m+6
=(m+4)2-10,
∵(m+4)2≥25,
∴(m+4)2-10≥15,
即代数式m2+2n2+6m+8的最小值等于15.
故答案为15.
点评 本题考查的是配方法的应用,掌握配方法的一般步骤是解题的关键,注意偶次方的非负性的应用.

练习册系列答案
相关题目
6.下列分解因式正确的是( )
| A. | -ma-m=-m(a-1) | B. | a2-1=(a-1)2 | C. | a2-6a+9=(a-3)2 | D. | a2+3a+9=(a+3)2 |
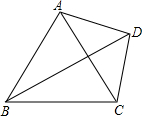 己知:如图,四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,且∠BAD+∠CAD=180°,那么∠BDC的度数为29°.
己知:如图,四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,且∠BAD+∠CAD=180°,那么∠BDC的度数为29°.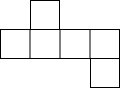 现有一张长为30cm,宽为20cm的长方形材料,若将其裁剪出一个如图所示的正方体表面展开图,要求使折叠后的正方体表面积最大,且正方体的棱长为整数,那么余料的面积是384cm2.
现有一张长为30cm,宽为20cm的长方形材料,若将其裁剪出一个如图所示的正方体表面展开图,要求使折叠后的正方体表面积最大,且正方体的棱长为整数,那么余料的面积是384cm2.