Question

13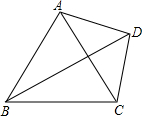．己知：如图，四边形ABCD中，对角线BD平分∠ABC，∠ACB=72°，∠ABC=50°，且∠BAD+∠CAD=180°，那么∠BDC的度数为29°．

Answer 1

分析 延长BA和BC，过D点作DE⊥BA于E点，过D点作DF⊥BC于F点，根据BD是∠ABC的平分线可得出△BDE≌△BDF，故DE=DF，过D点作DG⊥AC于G点，可得出△ADE≌△ADG，△CDG≌△CDF，进而得出CD为∠ACF的平分线，得出∠DCA=54°，再根据∠ADC=180°-∠DAC-∠DCA即可得出结论．

解答 解：延长BA和BC，过D点作DE⊥BA于E点，过D点作DF⊥BC于F点，
∵BD是∠ABC的平分线
在△BDE与△BDF中，
$\left\{\begin{array}{l}{∠ABD=∠CBD}\\{BD=BD}\\{∠AED=∠DFC}\end{array}\right.$，
∴△BDE≌△BDF（ASA），
∴DE=DF，
又∵∠BAD+∠CAD=180°
∠BAD+∠EAD=180°
∴∠CAD=∠EAD，
∴AD为∠EAC的平分线，
过D点作DG⊥AC于G点，
在Rt△ADE与Rt△ADG中，
$\left\{\begin{array}{l}{AD=AD}\\{DE=DG}\end{array}\right.$，
∴△ADE≌△ADG（HL），
∴DE=DG，
∴DG=DF．
在Rt△CDG与Rt△CDF中，
$\left\{\begin{array}{l}{CD=CD}\\{DG=DF}\end{array}\right.$，
∴Rt△CDG≌Rt△CDF（HL）
∴CD为∠ACF的平分线
∠ACB=72°
∴∠DCA=54°，
△ABC中，
∵∠ACB=72°，∠ABC=50°，
∴∠BAC=180°-72°-50°=58°，
∴∠DAC=180$\frac{180°-58°}{2}$=61°，
∴∠ADC=180°-∠DAC-∠DCA=180°-61°-54°=65°，
∴∠BDC=180°-25°-54°-72°=29°．
故答案为：29°．

点评 本题考查了角平分想的性质，以及三角形的全等和三角形的内角和定理，注意知识点的综合运用．