题目内容
8.在△ABC中,a=2,c=$\frac{4\sqrt{3}}{3}$,∠A=60°,则△ABC的面积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
分析 过B作BD⊥AC于D,在Rt△ABD中,根据sin∠A=$\frac{BD}{AB}$,求得BD=2,在Rt△CBD中,哟与BC=2,BD=2,得到BC⊥AC,于是得到结果.
解答 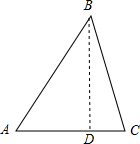 解:过B作BD⊥AC于D,
解:过B作BD⊥AC于D,
在Rt△ABD中,∵sin∠A=$\frac{BD}{AB}$,
∴$\frac{BD}{\frac{4\sqrt{3}}{3}}$=$\frac{\sqrt{3}}{2}$,
∴BD=2,∴AD=$\frac{2\sqrt{3}}{3}$,
在Rt△CBD中,∵BC=2,BD=2,
∴BC⊥AC,
∴S△ABC=$\frac{1}{2}•AC•BC$=$\frac{1}{2}×\frac{2\sqrt{3}}{3}×2$=$\frac{2\sqrt{3}}{3}$,
故选A.
点评 本题考查了解直角三角形,三角形的面积,熟记解直角三角形的定义是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
19.下列运算错误的是( )
| A. | a-2•a-1=a2 | B. | (a2)-3=a-6 | ||
| C. | a2÷a-3=a5 | D. | a-n=($\frac{1}{a}$)n(n为正整数) |
20.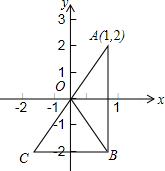 如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )
如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )
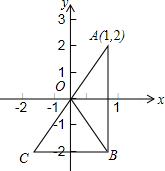 如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )
如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )| A. | (-1,-2) | B. | (1,-2) | C. | (-1,2) | D. | (-2,-1) |
17.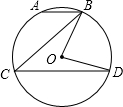 如图所示,在圆O中弦AB∥CD,若∠ABC=50°,则∠BOD等于( )
如图所示,在圆O中弦AB∥CD,若∠ABC=50°,则∠BOD等于( )
 如图所示,在圆O中弦AB∥CD,若∠ABC=50°,则∠BOD等于( )
如图所示,在圆O中弦AB∥CD,若∠ABC=50°,则∠BOD等于( )| A. | 50° | B. | 40° | C. | 100° | D. | 80° |
18.对于方程3x2-x-2=0,下列判断正确的是( )
| A. | 一次项系数为1 | B. | 常数项是2 | C. | 二次项系数是3x2 | D. | 一次项是-x |
 如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.
如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.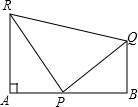 如图,RA⊥AB,QB⊥AB,P是AB上的一点,RP=PQ=a,RA=h,QB=k,∠RPA=75°,∠QPB=45°,求AB的长度.
如图,RA⊥AB,QB⊥AB,P是AB上的一点,RP=PQ=a,RA=h,QB=k,∠RPA=75°,∠QPB=45°,求AB的长度.