题目内容
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

解:(1)如图所示:C1(2,﹣2);
故答案为:(2,﹣2);
(2)如图所示:C2(1,0);
故答案为:(1,0);
(3)∵A2C22=20,B2C =20,A2B2
=20,A2B2 =40,
=40,
∴△A2B2C2是等腰直角三角形,
∴△A2B2C2的面积是: ×
× ×20=10平方单位.
×20=10平方单位.


练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
下列运算正确的是( )
|
| A. | a3+a3=a6 | B. | a6÷a2=a4 | C. | a3•a5=a15 | D. | (a3)4=a7 |
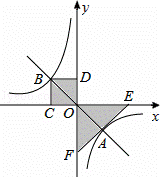
如图,过点O作直线与双曲线y= (k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
|
| A. | S1=S2 | B. | 2S1=S2 | C. | 3S1=S2 | D. | 4S1=S2 |
下列命题是假命题的是( )
|
| A. | 不在同一直线上的三点确定一个圆 |
|
| B. | 矩形的对角线互相垂直且平分 |
|
| C. | 正六边形的内角和是720° |
|
| D. | 角平分线上的点到角两边的距离相等 |
 .
.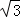 PC.(不必证明)
PC.(不必证明)