题目内容
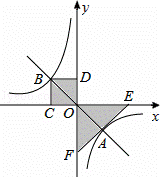
如图,过点O作直线与双曲线y= (k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
|
| A. | S1=S2 | B. | 2S1=S2 | C. | 3S1=S2 | D. | 4S1=S2 |
B
解:设A点坐标为(m,n),
过点O的直线与双曲线y= 交于A、B两点,则A、B两点关与原点对称,则B的坐标为(﹣m,﹣n);
交于A、B两点,则A、B两点关与原点对称,则B的坐标为(﹣m,﹣n);
矩形OCBD中,易得OD=﹣n,OC=m;则S1=﹣mn;
在Rt△EOF中,AE=AF,故A为EF中点,
由中位线的性质可得OF=﹣2n,OE=2m;
则S2=OF×OE=﹣4mn;
故2S1=S2

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
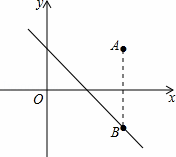
如图,在平面直角坐标系中,点A(2,m)在第一象限,若点A关于x轴的对称点B在直线y=﹣x+1上,则m的值为( )
|
| A. | ﹣1 | B. | 1 | C. | 2 | D. | 3 |


 .
.