题目内容
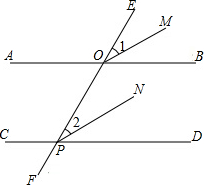已知AB，CD被直线EF所截，交点分别于O，P，OM平分∠EOB，PN平分∠OPD，如果∠1=∠2．（1）OM∥PN吗？为什么？
（2）AB∥CD吗？为什么？
考点：平行线的判定
专题：
分析：（1）∠1和∠2是OM、PN被直线EF所截得到的一对同位角，可判定OM∥PN；
（2）由角平分线的性质可得∠EOB=∠EPD，可判定AB∥CD．
（2）由角平分线的性质可得∠EOB=∠EPD，可判定AB∥CD．
解答：
解：
（1）OM∥PN，证明如下：
∵∠1=∠2，且∠1和∠2是OM、PN被直线EF所截得到的一对同位角，
∴OM∥PN；
（2）AB∥CD，证明如下：
∵OM平分∠EOB，PN平分∠OPD，
∴∠EOB=2∠1，∠EPD=2∠2，
∵∠1=∠2，
∴∠EOB=∠EPD，
∴AB∥CD．
（1）OM∥PN，证明如下：
∵∠1=∠2，且∠1和∠2是OM、PN被直线EF所截得到的一对同位角，
∴OM∥PN；
（2）AB∥CD，证明如下：
∵OM平分∠EOB，PN平分∠OPD，
∴∠EOB=2∠1，∠EPD=2∠2，
∵∠1=∠2，
∴∠EOB=∠EPD，
∴AB∥CD．
点评：本题主要考查平行线的判定，掌握平行线的性质和判定是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补，④a∥b，b∥c?a∥c．
练习册系列答案
相关题目
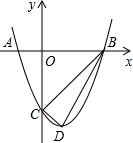如图，抛物线与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C（0，-3），设抛物线的顶点为D．（1）求该抛物线的解析式和顶点D的坐标；
（2）以B、C、D为顶点的三角形是直角三角形吗？为什么？
如图，不能推出a∥b的条件是（ ）| A、∠1=∠3 |
| B、∠1=∠4 |
| C、∠2=∠4 |
| D、∠2+∠3=180° |
如图所示，如果∠1=