题目内容
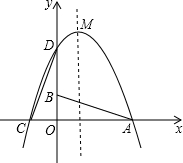 如图,已知△OAB的顶点A(3,0),B(0,1),O是坐标原点.将△OAB绕点O按逆时针旋转90°得到△ODC.
如图,已知△OAB的顶点A(3,0),B(0,1),O是坐标原点.将△OAB绕点O按逆时针旋转90°得到△ODC.(1)写出C,D两点的坐标;
(2)求过C,D,A三点的抛物线的解析式,并求此抛物线的顶点M的坐标;
(3)在线段AB上是否存在点N使得NA=NM?若存在,请求出点N的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据旋转的性质,可得OC=OB,OD=OA,进而可得CD两点的坐标;
(2)设出解析式,并将A、C、D三点的坐标代入可得方程组,解可得解析式,进而可得M的坐标;
(3)假设存在并设出其坐标,连接MB,作ME⊥y轴于E,可得ME、BE、MB的长,进而可得BA与MB的关系,即可求出N的坐标,故可作出判断.
(2)设出解析式,并将A、C、D三点的坐标代入可得方程组,解可得解析式,进而可得M的坐标;
(3)假设存在并设出其坐标,连接MB,作ME⊥y轴于E,可得ME、BE、MB的长,进而可得BA与MB的关系,即可求出N的坐标,故可作出判断.
解答:解:(1)C(-1,0),D(0,3).
(2)设所求抛物线的解析式为y=ax2+bx+c(a≠0)
∵A,C,D在抛物线上
∴
解得a=-1,b=2,c=3
即y=-x2+2x+3
又y=-(x-1)2+4
∴M(1,4).
(3)解:(法一)
连接MB,作ME⊥y轴于E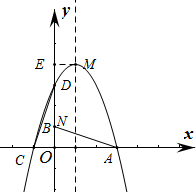 ,
,
则ME=1,BE=4-1=3,
∴MB=
,BA=MB,
即在线段AB上存在点N(0,1)(即点B)使得NA=NM.
(法二)
设在AB上存在点N(a,b)(0≤b≤1)使得NA=NM(即NA2=NM2)
作NP⊥OA于P,NQ⊥对称轴x=1于Q,
则
=
?3-a=3b,
∴NA2=b2+(3-a)2=10b2,
NM2=(1-a)2+(4-b)2=10b2-20b+20,
则10b2=10b2-20b+20,
∴b=1.
故在线段AB上存在点N(0,1)(即点B)使得NA=NM.
(2)设所求抛物线的解析式为y=ax2+bx+c(a≠0)
∵A,C,D在抛物线上
∴
|
即y=-x2+2x+3
又y=-(x-1)2+4
∴M(1,4).
(3)解:(法一)
连接MB,作ME⊥y轴于E
 ,
,则ME=1,BE=4-1=3,
∴MB=
| 10 |
即在线段AB上存在点N(0,1)(即点B)使得NA=NM.
(法二)
设在AB上存在点N(a,b)(0≤b≤1)使得NA=NM(即NA2=NM2)
作NP⊥OA于P,NQ⊥对称轴x=1于Q,
则
| b |
| 1 |
| 3-a |
| 3 |
∴NA2=b2+(3-a)2=10b2,
NM2=(1-a)2+(4-b)2=10b2-20b+20,
则10b2=10b2-20b+20,
∴b=1.
故在线段AB上存在点N(0,1)(即点B)使得NA=NM.
点评:本题考查二次函数综合题,涉及了旋转的性质、待定系数法求二次函数解析式、勾股定理等考点,解题的关键在于将二次函数的图象与解析式相结合,难度不大.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
单项式-xy2z3的系数及次数分别是( )
| A、系数是0,次数是5 |
| B、系数是1,次数是6 |
| C、系数是-1,次数是5 |
| D、系数是-1,次数是6 |
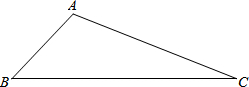 如图,在△ABC中,∠BAC是钝角,完成下列画图.(不写作法保留作图痕迹)
如图,在△ABC中,∠BAC是钝角,完成下列画图.(不写作法保留作图痕迹) 如图所示,在△ABC中,∠BAC是钝角,请在图中作出AB边上的高CF.
如图所示,在△ABC中,∠BAC是钝角,请在图中作出AB边上的高CF. 如图,∠1=∠2,∠C=∠D,求证:AC=AD.
如图,∠1=∠2,∠C=∠D,求证:AC=AD.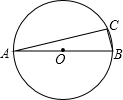 如图,AB是⊙O的直径,∠A=10°,则∠ABC=
如图,AB是⊙O的直径,∠A=10°,则∠ABC=