题目内容
 如图抛物线y=-x2+bx+c的图象与x轴的一个交点(1,0),则抛物线与x轴的另一个交点坐标是
如图抛物线y=-x2+bx+c的图象与x轴的一个交点(1,0),则抛物线与x轴的另一个交点坐标是考点:抛物线与x轴的交点
专题:
分析:根据抛物线与x轴交点关于对称轴对称,已知一个交点,即可求得另一个交点的坐标,即可解题.
解答:解:设另一个交点横坐标为x,
∵y=-x2+bx+c的对称轴为x=-1,
∴x+1=-1×2,
∴x=-3.
故答案为(-3,0).
∵y=-x2+bx+c的对称轴为x=-1,
∴x+1=-1×2,
∴x=-3.
故答案为(-3,0).
点评:本题考查了韦达定理的运用,考查了抛物线与x轴交点关于对称轴对称的性质,本题中运用韦达定理是解题的关键.

练习册系列答案
相关题目
在六边形内任取一点,把这个点与六边形的各顶点分别连接可以得到( )
| A、4个三角形 |
| B、5个三角形 |
| C、6个三角形 |
| D、7个三角形 |
 两块完全相同的等腰三角形放成如图样子,假设图形中的所有点、线、面都在同一平面内,指出图中相似不正确的是( )
两块完全相同的等腰三角形放成如图样子,假设图形中的所有点、线、面都在同一平面内,指出图中相似不正确的是( )| A、△DAE∽△DCA |
| B、△EAD∽△EBA |
| C、△BAD∽△CAE |
| D、△BAE∽△CDA |
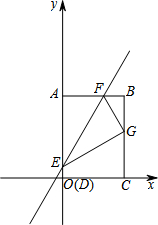 如图,四边形ABCD为矩形,点D与坐标原点重合,点C在x轴上,点A在y轴上,点B的坐标是(8,12),矩形ABCD沿直线EF折叠,点A落在BC边上的G处,点E,F分别在AD,AB上,且F点的坐标是(5,12).
如图,四边形ABCD为矩形,点D与坐标原点重合,点C在x轴上,点A在y轴上,点B的坐标是(8,12),矩形ABCD沿直线EF折叠,点A落在BC边上的G处,点E,F分别在AD,AB上,且F点的坐标是(5,12). 自行选取一组数构造一个三阶幻方,使得每行、每列、每条对角线上的三个数之和都等于45.
自行选取一组数构造一个三阶幻方,使得每行、每列、每条对角线上的三个数之和都等于45.