题目内容
11. 图中阴影部分的面积是35cm2,求圆环的面积.
图中阴影部分的面积是35cm2,求圆环的面积.
分析 根据题意设大圆的半径为R,小圆的半径为r,大三角形的面积为$\frac{1}{2}$R2,小三角形的面积为$\frac{1}{2}$r2,用大三角形的面积减去小三角形的面积可得R2-r2,代入圆环的面积公式S=π(R2-r2),得出答案.
解答 解:设大圆的半径为R,小圆的半径为r,
则大三角形的面积=$\frac{1}{2}$R2,小三角形的面积=$\frac{1}{2}$r2,
∵阴影部分的面积=大三角形的面积-小三角形的面积=$\frac{1}{2}$R2-$\frac{1}{2}$r2=$\frac{1}{2}$(R2-r2)=35,
∴R2-r2=70,
∴圆环的面积S=π(R2-r2)=70π.
点评 此题主要考查了圆环的面积公式,根据已知得出R2-r2是解答此题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
19.2015年春我国大部分地区出现严重雾霾,为了增强同学们的环保意识,某校组织了一次防治雾霾知识竞赛,两组学生成绩统计如下:
已知算得两个组的人均分数都是80分,请根据你所学过的统计知识,进一步判断这两个组这次成绩谁优谁次,并说明理由.
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
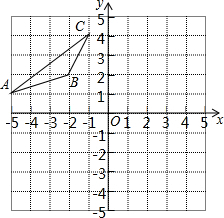 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图: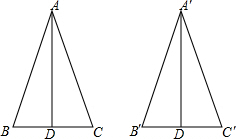 如图,AD、A′D′分别是BC和B′C′上的高,且∠B=∠B′,$\frac{A′D′}{AD}$=$\frac{B′C′}{BC}$,求证:△ABC∽△A′B′C.
如图,AD、A′D′分别是BC和B′C′上的高,且∠B=∠B′,$\frac{A′D′}{AD}$=$\frac{B′C′}{BC}$,求证:△ABC∽△A′B′C.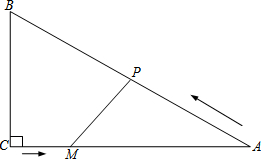 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M从点C出发,以每秒1cm的速度沿CA向终点A移动,同时动点P从点A出发,以每秒2cm的速度沿AB向终点B移动,连接PM,设移动时间为t(s)(0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M从点C出发,以每秒1cm的速度沿CA向终点A移动,同时动点P从点A出发,以每秒2cm的速度沿AB向终点B移动,连接PM,设移动时间为t(s)(0<t<2.5).