题目内容
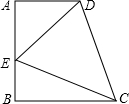 在直角梯形ABCD中,AD∥BC,(AD<BC),AB⊥BC,AB=BC=12,点E在AB边上,连接CE,DE,若∠DCE=45°,DE=10,则线段BE的长为
在直角梯形ABCD中,AD∥BC,(AD<BC),AB⊥BC,AB=BC=12,点E在AB边上,连接CE,DE,若∠DCE=45°,DE=10,则线段BE的长为考点:直角梯形
专题:
分析:过点C作CF⊥AD交AD的延长线于F,可得四边形ABCF是正方形,将△CBE绕点C顺时针旋转90°得到△FCG,根据旋转的性质得CE=CG,BE=FG,∠BCE=∠FCG,然后求出∠DCG=∠DCE=45°,再利用“边角边”证明△CDE和△CDG全等,根据全等三角形对应边相等可得DE=DG,设BE=x,表示出AE、DF、AD,然后在Rt△ADE中,利用勾股定理列出方程求解即可.
解答: 解:如图,过点C作CF⊥AD交AD的延长线于F,
解:如图,过点C作CF⊥AD交AD的延长线于F,
∵AD∥BC,AB⊥BC,AB=BC,
∴四边形ABCF是正方形,
∴CF=BC,
将△CBE绕点C顺时针旋转90°得到△FCG,
由旋转的性质得,CE=CG,BE=FG,∠BCE=∠FCG,
∵∠DCE=45°,
∴∠DCG=∠DCE=45°,
在△CDE和△CDG中,
,
∴△CDE≌△CDG(SAS),
∴DE=DG,
设BE=x,则AE=12-x,DF=10-x,
AD=12-(10-x)=2+x,
在Rt△ADE中,AE2+AD2=DE2,
∴(12-x)2+(2+x)2=102,
整理得,x2-10x+24=0,
解得x1=4,x2=6,
所以线段BE的长为4或6.
故答案为:4或6.
 解:如图,过点C作CF⊥AD交AD的延长线于F,
解:如图,过点C作CF⊥AD交AD的延长线于F,∵AD∥BC,AB⊥BC,AB=BC,
∴四边形ABCF是正方形,
∴CF=BC,
将△CBE绕点C顺时针旋转90°得到△FCG,
由旋转的性质得,CE=CG,BE=FG,∠BCE=∠FCG,
∵∠DCE=45°,
∴∠DCG=∠DCE=45°,
在△CDE和△CDG中,
|
∴△CDE≌△CDG(SAS),
∴DE=DG,
设BE=x,则AE=12-x,DF=10-x,
AD=12-(10-x)=2+x,
在Rt△ADE中,AE2+AD2=DE2,
∴(12-x)2+(2+x)2=102,
整理得,x2-10x+24=0,
解得x1=4,x2=6,
所以线段BE的长为4或6.
故答案为:4或6.
点评:本题考查了直角梯形,正方形的性质,旋转的性质,全等三角形的判定与性质,勾股定理的应用,难点在于作辅助线构造出全等三角形并利用勾股定理列出方程.

练习册系列答案
相关题目
已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,则当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 2 | 1 | 2 | … |
| A、y1<y2 |
| B、y1>y2 |
| C、y1≥y2 |
| D、y1≤y2 |
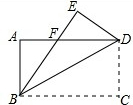 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,CD=3cm,CB=4cm,则△BFD的面积为
如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,CD=3cm,CB=4cm,则△BFD的面积为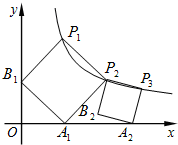 正方形的A1B1P1P2顶点P1、P2在反比例函数y=
正方形的A1B1P1P2顶点P1、P2在反比例函数y=