题目内容
19.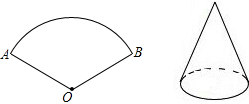 如图,将弧长为6π,圆心角为120°的圆形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是6$\sqrt{2}$.
如图,将弧长为6π,圆心角为120°的圆形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是6$\sqrt{2}$.
分析 根据弧长求得圆锥的底面半径和扇形的半径,利用勾股定理求得圆锥的高即可.
解答 解:∵弧长为6π,
∴底面半径为6π÷2π=3,
∵圆心角为120°,
∴$\frac{120πR}{180}$=6π,
解得:R=9,
∴圆锥的高为$\sqrt{{9}^{2}-{3}^{2}}$=6$\sqrt{2}$,
故答案为:6$\sqrt{2}$.
点评 本题考查了圆锥的计算,解题的关键是能够利用圆锥的底面周长等于侧面展开扇形的弧长求得圆锥的底面半径,难度一般.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
7.甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别在A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200).
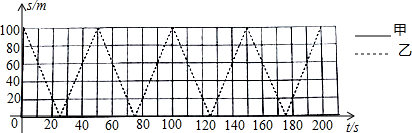
(2)根据(1)中所画图象,完成下列表格:
(3)①直接写出甲、乙两人分别在第一个100m内,t与s的函数解析式,并指出自变量t的取值范围.
②求甲、乙第6次相遇时t的值.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200).

(2)根据(1)中所画图象,完成下列表格:
| 两人相遇次数(单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和(单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
②求甲、乙第6次相遇时t的值.
4.2015年我国大学生毕业人数将达到7 490 000人,这个数据用科学记数法表示为( )
| A. | 7.49×107 | B. | 7.49×106 | C. | 74.9×105 | D. | 0.749×107 |
14.下列是二元一次方程的是( )
| A. | 3x+4=9 | B. | $\frac{1}{x}+\frac{2}{3y}=2$ | C. | x2+y=0 | D. | 6x+1=y |
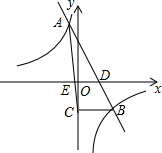 一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A(-1,4),B(2,n)两点,直线AB交x轴于点D.
一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A(-1,4),B(2,n)两点,直线AB交x轴于点D.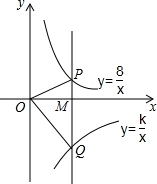 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=$\frac{8}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象交于P、Q两点,若S△POQ=14,则k的值为-20.
如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=$\frac{8}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象交于P、Q两点,若S△POQ=14,则k的值为-20.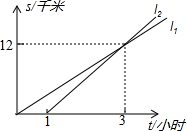 A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/小时;④乙先到达B地.其中正确的个数是( )
A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/小时;④乙先到达B地.其中正确的个数是( ) 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC=12cm.
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC=12cm.