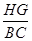题目内容
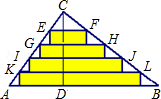
 如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.若将斜边上的高CD n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是________cm2.
如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.若将斜边上的高CD n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是________cm2.
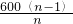
分析:由△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm由勾股定理即可求得AB的长,然后利用三角形的面积,求得高CD的长,继而可求得纸条宽度,然后利用相似三角形的对应边成比例,即可求得EF,GH以及KL的长,继而求得这(n-1)张纸条的面积和.
解答:
 解:∵△ABC是直角三角形,AC=30cm,BC=40cm.
解:∵△ABC是直角三角形,AC=30cm,BC=40cm.∴AB=
 =50(cm),
=50(cm),∵S△ABC=
 AC•BC=
AC•BC= AB•CD,
AB•CD,∴AC•BC=AB•CD,
∴30×40=50•CD,
∴CD=24cm.
可知纸条宽度为:
 cm,
cm,∵EF∥AB,
∴△CEF∽△CAB,
∴
 =
= ,
,∴EF=
 AB,
AB,同理:GH=
 AB,KL=
AB,KL= AB,
AB,∴(n-1)张纸条的面积和为:
(EF+GH+…+KL)•

=(
 +
+ +…+
+…+ )×50×
)×50×
=
 [1+2+…+(n-1)]×50×
[1+2+…+(n-1)]×50×
=
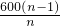 (cm2).
(cm2).故答案为:
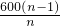 .
.点评:此题考查了相似三角形的判定与性质与勾股定理的应用.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
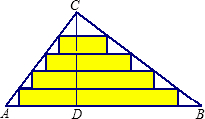 如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.
如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.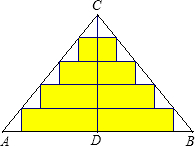 如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40cm.
如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40cm.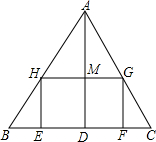 一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.
一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.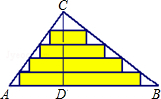 (2013•江阴市一模)如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.若将斜边上的高CD n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是
(2013•江阴市一模)如图,△ABC是一张直角三角形彩色纸,AC=30cm,BC=40cm.若将斜边上的高CD n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是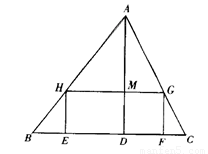
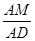 =
=