题目内容
14.已知4x-3y-6z=0,x+2y-7z=0,且x,y,z≠0,求$\frac{2x+3y+6z}{x+5y+7z}$的值.分析 由已知的式子利用加减法,得到x和y的关系,然后代入所求的分式,分子的分母都用同一个字母表示,约分即可求解.
解答 解:由4x-3y-6z=0得:4x=3y+6z…①,
由x+2y-7z=0得7z=x+2y…②,
把②代入①得:2x=3y…③,
则原式=$\frac{2x+3y+6z}{x+5y+7z}$=$\frac{2x+4x}{x+5y+x+2y}$=$\frac{6x}{2x+7y}$=$\frac{6x}{2x+\frac{14}{3}x}$=$\frac{9}{10}$.
点评 本题考查了分式的化简求值,正确对分子和分母进行变形,转化为用一个字母表示的形式是关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

 如图,抛物线的顶点A(-3,-3),且经过原点O.
如图,抛物线的顶点A(-3,-3),且经过原点O.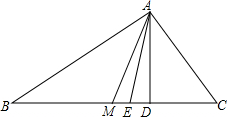 已知:如图,在△ABC中,AB>AC,AM是中线,AD是高,AE是角平分线,并且∠DAE=∠MAE,求证:∠BAC=90°.
已知:如图,在△ABC中,AB>AC,AM是中线,AD是高,AE是角平分线,并且∠DAE=∠MAE,求证:∠BAC=90°.