题目内容
14. 如图,在Rt△ABC中,∠C=90°,CD是斜边上的高,已知AD=2.8cm,BD=1.4cm,试求高CD的长(精确到0.01cm)
如图,在Rt△ABC中,∠C=90°,CD是斜边上的高,已知AD=2.8cm,BD=1.4cm,试求高CD的长(精确到0.01cm)
分析 根据勾股定理得出AB2=AC2+BC2=AD2+CD2+BD2+CD2,进而解答即可.
解答 解:∵在Rt△ABC中,∠C=90°,CD是斜边上的高,
∴在Rt△ABC中,AB2=AC2+BC2,
在Rt△ADC中,AC2=AD2+CD2,
在Rt△DBC中,BC2=CD2+DB2,
可得:AB2=AC2+BC2=AD2+CD2+BD2+CD2,
即(2.8+1.4)2=2.82+1.42+2CD2,
解得:CD=1.98cm.
点评 此题考查勾股定理问题,关键是根据勾股定理得出AB2=AC2+BC2=AD2+CD2+BD2+CD2.

练习册系列答案
相关题目
5.一个多边形的内角和的度数是外角和的2倍,则这个多边形是( )
| A. | 三角形 | B. | 四边形 | C. | 六边形 | D. | 八边形 |
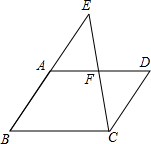 如图,在?ABCD中,点E在BA的延长线上,连结CE交AD于点F,且F是AD的中点,求证:AE=CD.
如图,在?ABCD中,点E在BA的延长线上,连结CE交AD于点F,且F是AD的中点,求证:AE=CD. 如图,∠1是△ABC的一个外角,∠2=∠BAC+∠BCA,∠1+∠2+∠3=360°.
如图,∠1是△ABC的一个外角,∠2=∠BAC+∠BCA,∠1+∠2+∠3=360°.