题目内容
12.⊙O的半径为5,弦BC=8,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为2或8.分析 根据题意画出图形,连接OB,由垂径定理可知BD=$\frac{1}{2}$BC,在Rt△OBD中,根据勾股定理求出OD的长,进而可得出结论.
解答 解: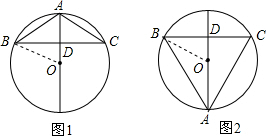 如图所示,连接OB,
如图所示,连接OB,
∵⊙O的半径为5,弦BC=8,AB=AC,
∴AD⊥BC,
∴BD=$\frac{1}{2}$BC=4,
在Rt△OBD中,
∵BD2+OD2=OB2,即42+OD2=52,
解得,OD=3,
∴当如图1所示时,AD=OA-OD=5-3=2;
当如图2所示时,AD=OA+OD=5+3=8,
故答案为:2或8.
点评 本题考查的是垂径定理的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键,在解答此题时要进行分类讨论.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
2.下列实数中,是无理数的为( )
| A. | $-\sqrt{5}$ | B. | $\frac{1}{5}$ | C. | 0 | D. | -5 |
17.若代数式x2-10x+k是一个完全平方式,则k=( )
| A. | 25 | B. | 25或-25 | C. | 10 | D. | 5或-5 |
 △ABC在直角坐标系中的位置如图所示,直线l经过点(1,0),并且与x轴垂直,△A1B1C1与△ABC关于线l对称.
△ABC在直角坐标系中的位置如图所示,直线l经过点(1,0),并且与x轴垂直,△A1B1C1与△ABC关于线l对称. 如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.
如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.