题目内容
4. 已知,如图,在?ABCD中,AE=CF,点M、N是ED、BF的中点,求证:EN∥MF.
已知,如图,在?ABCD中,AE=CF,点M、N是ED、BF的中点,求证:EN∥MF.
分析 根据平行四边的性质,可得AB、与CD的关系,再根据平行四边性的判定,可得EBFD的形状,根据平行四边形的性质,可得ED与BF的关系,根据一组对边平行且相等的四边形是平行四边,可得ENFM的形状,再根据平行四边性的性质,可得答案.
解答 证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
∵AE=CF,
∴BE=DF,BE∥DF,
∴四边形EBFD是平行四边形,
∴ED∥BF,ED=BF.
∵点M、N是ED、BF的中点,
∴EM=NF.∵EM∥NF,
∴四边形ENFM是平,
∴EN∥MF.
点评 本题考查了平行线的判定与性质,正确区分平行线的判定与性质是解题关键.

练习册系列答案
相关题目
19.将代数式x2+6x-2化成(x+p)2+q的形式为( )
| A. | (x-3)2+11 | B. | (x+3)2-1 | C. | (x+3)2-11 | D. | (x+2)2+4 |
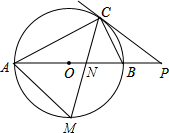 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠ACB的平分线CM分别与AB,⊙O交于点N,M,且PC=PN.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠ACB的平分线CM分别与AB,⊙O交于点N,M,且PC=PN. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题: 如图,在△ABC中,BD⊥AC,AB=6,$AC=5\sqrt{3}$,∠A=30°
如图,在△ABC中,BD⊥AC,AB=6,$AC=5\sqrt{3}$,∠A=30°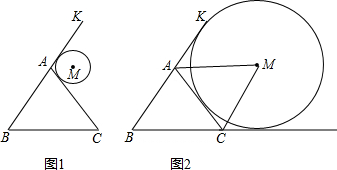
 如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )