题目内容
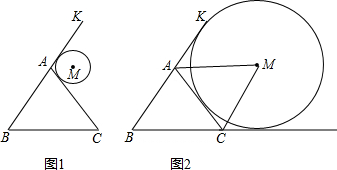
16.已知等腰△ABC和⊙M,且AB=AC.(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证:AM∥BC;
(2)如图2,若∠B=60°,⊙M与BA的延长线AK、BC的延长线CE及边AC均相切,求证:四边形ABCM是平行四边形.
分析 (1)由等边△ABC,即可得∠B=∠BAC=60°,求得∠KAC=120°,又由⊙M与BA的延长线AK及边AC均相切,利用切线长定理,即可得∠KAM=60°,然后根据同位角相等,两直线平行,证得AM∥BC;
(2)根据(1),易证得AM∥BC,CM∥AB,继而可证得四边形ABCM是平行四边形.
解答 证明:
(1)连接AM,如图1,
∵AB=AC,∴∠B=∠ACB.
∵⊙M与BA的延长线AK及边AC均相切,
∴∠KAM=∠CAM=$\frac{1}{2}$∠KAC,
又∠KAC=∠B+∠ACB,
∴∠B=$\frac{1}{2}$∠KAC.
∴∠KAM=∠B.
∴AM∥BC.
(2)∵AB=AC,∠B=60°,如图2,
∴△ABC是等边三角形,
即∠B=∠BAC=∠ACB=60°.
∴∠KAC=180°-∠BAC=120°,∠FCA=120°,
∵⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,
∴∠KAM=∠CAM=$\frac{1}{2}$∠KAC=$\frac{1}{2}$×l20°=60°,
∠KCM=∠ACM=$\frac{1}{2}$∠KCA=$\frac{1}{2}$×l20°=60°,
∴∠KAM=∠B=60°,∠FCM=∠B=60°.
∴AM∥BC,CM∥AB.
∴四边形ABCM是平行四边形.
点评 此题考查了切线长定理、平行线的判定以及等边三角形的判定和性质性质、平行四边形的判定,题目的综合性较强,难度中等,对学生的综合解题能力要求很高,解题的关键是熟记和圆有关的性质定理以及平行四边形的各种判定方法.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
5.下列各式中,正确的是( )
| A. | $\sqrt{4}=±2$ | B. | $±\sqrt{4}=2$ | C. | $\root{3}{8}=2$ | D. | $\sqrt{{{(-4)}^2}}=-4$ |
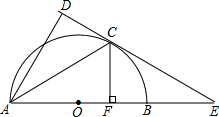 如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E. 已知,如图,在?ABCD中,AE=CF,点M、N是ED、BF的中点,求证:EN∥MF.
已知,如图,在?ABCD中,AE=CF,点M、N是ED、BF的中点,求证:EN∥MF.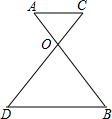 如图,已知:AB与CD相交于O,AC∥BD,$\frac{AO}{BO}$=$\frac{3}{5}$,则$\frac{CO}{CD}$的值为$\frac{3}{8}$.
如图,已知:AB与CD相交于O,AC∥BD,$\frac{AO}{BO}$=$\frac{3}{5}$,则$\frac{CO}{CD}$的值为$\frac{3}{8}$.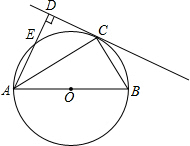 如图,AB为⊙O的直径,过点C作⊙O的切线,AD垂直切线于D,交⊙O于点E.
如图,AB为⊙O的直径,过点C作⊙O的切线,AD垂直切线于D,交⊙O于点E.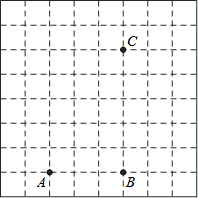 根据要求画图或作答.如图所示,已知点A、B、C是网格纸上的三个格点.
根据要求画图或作答.如图所示,已知点A、B、C是网格纸上的三个格点.