题目内容
某实验学校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,求出所有的购买方案;
(3)设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W元,求出W与x的函数关系式;并确定哪种方案投入资金最少,最少资金是多少?
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,求出所有的购买方案;
(3)设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W元,求出W与x的函数关系式;并确定哪种方案投入资金最少,最少资金是多少?
考点:一次函数的应用,二元一次方程组的应用,一元一次不等式组的应用
专题:
分析:(1)设两人学习桌单价x元,三人学习桌单价y元,然后列出方程组求解即可;
(2)设两人学习桌买m张,然后根据钱数和人数列出不等式组,求解得到x的取值范围,再写出所有的购买方案即可;
(3)根据总费用=两人学习桌和三人学习桌的费用之和列出关系式,再根据一次函数的增减性解答.
(2)设两人学习桌买m张,然后根据钱数和人数列出不等式组,求解得到x的取值范围,再写出所有的购买方案即可;
(3)根据总费用=两人学习桌和三人学习桌的费用之和列出关系式,再根据一次函数的增减性解答.
解答:解:(1)设两人学习桌单价x元,三人学习桌单价y元,
根椐题意,有
,
解得
.
答:两人学习桌单价50元,三人学习桌单价70元;
(2)设两人学习桌买m张,则三人学习桌买(98-m)张,
根据题意,有
,
解得:43≤m≤46,
∵m为正整数,
∴m=43,44,45,46共有4种方案,
分别是两人桌43张,三人桌55张;两人桌44张,三人桌54张;两人桌45张,三人桌53张;两人桌46张,三人桌52张;
(3)根据题意,得W=50x+70(98-x),
∴w=-20x+6860,
∵k=-20<0,
∴w随x的增大而减少,
当x=46时,w最小,
∴w最小=-20×46+6860=5940(元).
答:当两人桌买46张,三人桌买52张时,投入资金最少,最少资金5940元.
根椐题意,有
|
解得
|
答:两人学习桌单价50元,三人学习桌单价70元;
(2)设两人学习桌买m张,则三人学习桌买(98-m)张,
根据题意,有
|
解得:43≤m≤46,
∵m为正整数,
∴m=43,44,45,46共有4种方案,
分别是两人桌43张,三人桌55张;两人桌44张,三人桌54张;两人桌45张,三人桌53张;两人桌46张,三人桌52张;
(3)根据题意,得W=50x+70(98-x),
∴w=-20x+6860,
∵k=-20<0,
∴w随x的增大而减少,
当x=46时,w最小,
∴w最小=-20×46+6860=5940(元).
答:当两人桌买46张,三人桌买52张时,投入资金最少,最少资金5940元.
点评:本题考查了一次函数的应用,二元一次方程组的应用,一元一次不等式组的应用,读懂题目信息,找出题中等量关系和不等关系是解题的关键.

练习册系列答案
相关题目
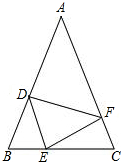 如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.
如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB. 足球训练场上教练在球门前划了一个圆圈进行无人防守的射门训练如图,甲,乙两名运动员分别在C,D两处,他们争论不休,都说在自已所在的位置对球门AB的张角大,如果你是教练,请评一评他们两个人谁的位置对球门AB的张角大?为什么?
足球训练场上教练在球门前划了一个圆圈进行无人防守的射门训练如图,甲,乙两名运动员分别在C,D两处,他们争论不休,都说在自已所在的位置对球门AB的张角大,如果你是教练,请评一评他们两个人谁的位置对球门AB的张角大?为什么?