Question

【题目】如图，矩形OBCD中，OB＝5，OD＝3，以O为原点建立平面直角坐标系，点B，点D分别在x轴，y轴上，点C在第一象限内，若平面内有一动点P，且满足S△POB＝S矩形OBCD，问：

（1）当点P在矩形的对角线OC上，求点P的坐标；

（2）当点P到O，B两点的距离之和PO+PB取最小值时，求点P的坐标．

Answer 1

【答案】（1）P（，2）；（2）（，2）或（﹣，2）

【解析】

（1）根据已知条件得到C（5，3），设直线OC的解析式为y＝kx，求得直线OC的解析式为y＝x，设P（m，m），根据S△POB＝S矩形OBCD，列方程即可得到结论；

（2）设点P的纵坐标为h，得到点P在直线y＝2或y＝﹣2的直线上，作B关于直线y＝2的对称点E，则点E的坐标为（5，4），连接OE交直线y＝2于P，则此时PO+PB的值最小，设直线OE的解析式为y＝nx，于是得到结论．

（1）如图：

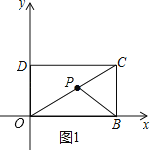
∵矩形OBCD中，OB＝5，OD＝3，

∴C（5，3），

设直线OC的解析式为y＝kx，

∴3＝5k，

∴k＝，

∴直线OC的解析式为y＝x，

∵点P在矩形的对角线OC上，

∴设P（m，m），

∵S△POB＝S矩形OBCD，

∴5×m＝3×5，

∴m＝，

∴P（，2）；

（2）∵S△POB＝S矩形OBCD，

∴设点P的纵坐标为h，

∴h×5＝5，

∴h＝2，

∴点P在直线y＝2或y＝﹣2上，

作B关于直线y＝2的对称点E，

则点E的坐标为（5，4），

连接OE交直线y＝2于P，则此时PO+PB的值最小，

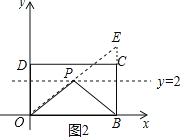
设直线OE的解析式为y＝nx，

∴4＝5n，

∴n＝，

∴直线OE的解析式为y＝x，

当y＝2时，x＝，

∴P（，2），

同理，点P在直线y＝﹣2上，

P（，﹣2），

∴点P的坐标为（，2）或（﹣，2）．