题目内容
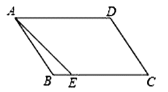
【题目】如图，菱形ABCD的对角线AC和BD相交于点O，AB＝
，OA＝a，OB＝b，且a，b满足：
．
（1）求菱形ABCD的面积；
（2）求
的值．
【答案】（1）4；（2）
【解析】
（1）首先根据菱形的性质得到AC和BD垂直平分，结合题意可得a2+b2＝5，进而得到ab＝2，结合图形的面积公式即可求出面积；
（2）根据a2+b2＝5，ab＝2得到a+b的值，进而求出答案．
解：（1）∵四边形ABCD是菱形，
∴BD垂直平分AC，
∵OA＝a，OB＝b，AB＝
，
∴a2+b2＝5，
∵a，b满足：
．
∴a2b2＝4，
∴ab＝2，
∴△AOB的面积＝
ab＝1，
∴菱形ABCD的面积＝4△AOB的面积＝4；
（2）∵a2+b2＝5，ab＝2，
∴（a+b）2＝a2+b2+2ab＝7，
∴a+b＝
，
∴
＝．
练习册系列答案
天天向上口算本系列答案
相关题目
