题目内容
已知函数y=ax2+bx+c中a＜0，b＞0，c＜0，△＜0，画出函数的大致图象．
考点：二次函数图象与系数的关系
专题：
分析：根据已知条件“a＜0、b＞0、c＜0，△＜0”判断出该函数图象的开口方向、与x轴和y轴的交点、对称轴所在的位置，然后据此来画出该函数的大致图象．
解答：解：∵a＜0，
∴抛物线开口方向向下．
∵a＜0，b＞0，则ab＜0，
∴该抛物线的对称轴在y轴的左侧．
∵c＜0，
∴该抛物线与y轴交于负半轴．
∵△＜0，
∴该抛物线与x轴没有交点，
故其图象如图所示：
．
∴抛物线开口方向向下．
∵a＜0，b＞0，则ab＜0，
∴该抛物线的对称轴在y轴的左侧．
∵c＜0，
∴该抛物线与y轴交于负半轴．
∵△＜0，
∴该抛物线与x轴没有交点，
故其图象如图所示：
．点评：本题考查了二次函数图象与系数的关系．根据二次函数y=ax2+bx+c系数符号判断抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数．
练习册系列答案
阅读快车系列答案
相关题目
用配方法解方程x2-2x-3=0时，配方后得到的方程为（ ）
| A、（x-1）2=4 |
| B、（x-1）2=-4 |
| C、（x+1）2=4 |
| D、（x+1）2=-4 |
如图，在由边长相同的正方形组成的网格中，A、B、C、D都是小正方形的顶点，AB、CD相交于点P，CE⊥AB于E，则sin∠APD=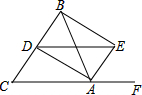
如图，△ABC中，AB=AC，F是CA延长线上一点，AD、AE分别平分∠BAC和∠BAF，BE⊥AE，说明：AB=DE．
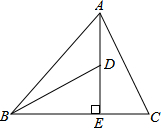已知在△ABC中，AE⊥BC于E，AE=BE，D是AE上一点，且DE=CE，连接BD，AC，试判断BD与AC的位置关系与数量关系，并说明理由．