题目内容
 已知如图,AD平分∠BAC,∠BAC+∠ACD=180°,点E在AD上,BE的延长线交CD于F,连CE,且AB=AC.求证:∠1=∠2.
已知如图,AD平分∠BAC,∠BAC+∠ACD=180°,点E在AD上,BE的延长线交CD于F,连CE,且AB=AC.求证:∠1=∠2.考点:全等三角形的判定与性质
专题:证明题
分析:求出∠CAE=∠BAE,根据SAS推出△CAE≌△BAE,根据全等得出∠2=∠B,求出CD∥AB,推出∠1=∠B即可.
解答:证明:∵AD平分∠BAC,
∴∠CAE=∠BAE,
在△CAE和△BAE中
∴△CAE≌△BAE,
∴∠2=∠B,
∵∠BAC+∠ACD=180°,
∴CD∥AB,
∴∠1=∠B,
∴∠1=∠2.
∴∠CAE=∠BAE,
在△CAE和△BAE中
|
∴△CAE≌△BAE,
∴∠2=∠B,
∵∠BAC+∠ACD=180°,
∴CD∥AB,
∴∠1=∠B,
∴∠1=∠2.
点评:本题考查了全等三角形的性质和判定,平行线的现在在和判定的应用,解此题的关键是推出∠2=∠B,∠1=∠B.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
某厂一月份生产产品50台,计划二、三月份共生产产品120台,设二、三月份平均每月增长率为x,根据题意,可列出方程为( )
| A、50(1+x)2=60 |
| B、50(1+x)2=120 |
| C、50+50(1+x)+50(1+x)2=120 |
| D、50(1+x)+50(1+x)2=120 |
 如图,在由边长相同的正方形组成的网格中,A、B、C、D都是小正方形的顶点,AB、CD相交于点P,CE⊥AB于E,则sin∠APD=
如图,在由边长相同的正方形组成的网格中,A、B、C、D都是小正方形的顶点,AB、CD相交于点P,CE⊥AB于E,则sin∠APD=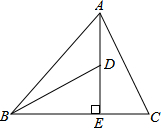 已知在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,连接BD,AC,试判断BD与AC的位置关系与数量关系,并说明理由.
已知在△ABC中,AE⊥BC于E,AE=BE,D是AE上一点,且DE=CE,连接BD,AC,试判断BD与AC的位置关系与数量关系,并说明理由.
 一艘轮船以18海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°的方向上,两小时后,轮船在B处测得小岛P在北偏西30°的方向上,已知小岛周围20海里内有暗礁,若轮船仍按原来方向继续前行,有无触礁的危险?
一艘轮船以18海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°的方向上,两小时后,轮船在B处测得小岛P在北偏西30°的方向上,已知小岛周围20海里内有暗礁,若轮船仍按原来方向继续前行,有无触礁的危险?