题目内容
 如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
考点:相似三角形的判定与性质
专题:
分析:(1)利用已知条件易证AB∥DE,进而证明△DCE∽△BCA;
(2)首先证明AE=DE,设DE=x,所以CE=AC-AE=AC-DE=4-x,利用(1)中相似三角形的对应边成比例即可求出x的值,即DE的长.
(2)首先证明AE=DE,设DE=x,所以CE=AC-AE=AC-DE=4-x,利用(1)中相似三角形的对应边成比例即可求出x的值,即DE的长.
解答:(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DA,
∵∠EAD=∠ADE,
∴∠BAD=∠ADE,
∴AB∥DE,
∴△DCE∽△BCA;
(2)解:∵∠EAD=∠ADE,
∴AE=DE,
设DE=x,
∴CE=AC-AE=AC-DE=4-x,
∵△DCE∽△BCA,
∴DE:AB=CE:AC,
即x:3=(4-x):4,
解得:x=
,
∴DE的长是
.
∴∠BAD=∠DA,
∵∠EAD=∠ADE,
∴∠BAD=∠ADE,
∴AB∥DE,
∴△DCE∽△BCA;
(2)解:∵∠EAD=∠ADE,
∴AE=DE,
设DE=x,
∴CE=AC-AE=AC-DE=4-x,
∵△DCE∽△BCA,
∴DE:AB=CE:AC,
即x:3=(4-x):4,
解得:x=
| 12 |
| 7 |
∴DE的长是
| 12 |
| 7 |
点评:本题考查了相似三角形的判定和性质、平行线的判定和性质、等腰三角形的判定和性质,题目的综合性较强,难度不大.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,在△ABC中,AB=AC,D是AB的中点,且DE⊥AB于点D,AB=10,BC=4,则△BEC的周长( )
如图,在△ABC中,AB=AC,D是AB的中点,且DE⊥AB于点D,AB=10,BC=4,则△BEC的周长( )| A、14 | B、6 | C、9 | D、12 |
如果把分式
中的x和y都扩大10倍,则分式的值( )
| x+y |
| xy |
| A、扩大10倍 | B、缩小10倍 |
| C、不变 | D、扩大100倍 |
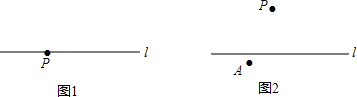 我们知道“经过一点有且只有一条直线与已知直线垂直”,那么如何用(不带刻度)直尺和圆规来作图呢?
我们知道“经过一点有且只有一条直线与已知直线垂直”,那么如何用(不带刻度)直尺和圆规来作图呢?