题目内容
8. 如图,点C是AB为直径的半圆上一点(O为圆心),以AC、BC为边向上作正方形ACDE和正方形BCFG,点P是DF的中点.若OP=6$\sqrt{2}$,AB=10,则△ABC的面积=( )
如图,点C是AB为直径的半圆上一点(O为圆心),以AC、BC为边向上作正方形ACDE和正方形BCFG,点P是DF的中点.若OP=6$\sqrt{2}$,AB=10,则△ABC的面积=( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
分析 连接AD、BF,设AC=a,BC=b,首先证明AD+BF=2OP,得a+b=12,再根据a2+b2=100求出$\frac{1}{2}$ab即可解决问题.
解答 解: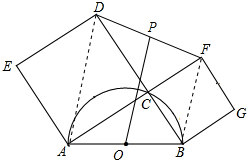 如图,连接AD、BF.设AC=a,BC=b,
如图,连接AD、BF.设AC=a,BC=b,
∵AB是直径,
∴∠ACB=90°
∵四边形ACDE、四边形BCFG都是正方形,
∴∠ACD=∠BCF=∠ACB=90°,
∴A、C、F共线,B、C、D共线,
∴∠DAC=∠BFC=45°,
∴AD∥BF,
∵DP=PF,AO=OB,
∴AD+BF=2PO,
∴$\sqrt{2}$a+$\sqrt{2}$b=12$\sqrt{2}$,
∴a+b=12,
又∵a2+b2=100,
∴a2+2ab+b2=144,
∴2ab=44,
∴S△ABC=$\frac{1}{2}$ab=11,
故选B.
点评 本题考查正方形的性质、图象、中位线定理,勾股定理等知识,解题的关键是添加辅助线,构造梯形,利用梯形中位线解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知点A(-3,a)、B(-1,b)、C(2,c)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,则且a、b、c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | c>a>b |
10.下列运算正确的是( )
| A. | a2+a2=a4 | B. | (a+b)2=a2+b2 | C. | $\sqrt{9}$=±3 | D. | (-a2)3=-a6 |
20.若x、y为有理数,且x≠0,若x+y=0,则($\frac{y}{x}$)2015的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2015 |
 如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°.
如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°. 如图,已知AD⊥BC,EF⊥BC,∠4=∠C,试证明∠1=∠2.
如图,已知AD⊥BC,EF⊥BC,∠4=∠C,试证明∠1=∠2.