题目内容
18. 如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点P是AC延长线上的一个动点,过点P作PE⊥AD,垂足为E,作CD延长线的垂线,垂足为E,则|PE-PF|=4.8.
如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点P是AC延长线上的一个动点,过点P作PE⊥AD,垂足为E,作CD延长线的垂线,垂足为E,则|PE-PF|=4.8.
分析 延长BC交PE于G,由菱形的性质得出AD∥BC,OA=OC=$\frac{1}{2}$AC=3,OB=OD=$\frac{1}{2}$BD=4,AC⊥BD,∠ACB=∠ACD,由勾股定理求出AD,由对顶角相等得出∠PCF=∠PCG,由菱形的面积的两种计算方法求出EG,由角平分线的性质定理得出PG=PF,得出PE-PF=PE-PG=EG即可.
解答 解:延长BC交PE于G,如图所示:
∵四边形ABCD是菱形,
∴AD∥BC,OA=OC=$\frac{1}{2}$AC=3,OB=OD=$\frac{1}{2}$BD=4,AC⊥BD,∠ACB=∠ACD,
∴AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=5,∠PCF=∠PCG,
∵菱形的面积=AD•EG=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6×8=24,
∴EG=4.8,
∵PE⊥AD,
∴PE⊥BG,
∵PF⊥DF,
∴PG=PF,
∴PE-PF=PE-PG=EG=4.8.
故答案为:4.8.
点评 本题考查了菱形的性质、勾股定理、角平分线的性质定理、菱形面积的计算等知识;本题综合性强,有一定难度,通过作辅助线证出PG=PF是解决问题的关键.

练习册系列答案
相关题目
9.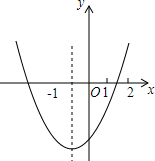 对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:
对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:
①abc<0;②16a-4b+c<0;③ax2+bx≥a-b;④3a+c<0.
其中,正确结论的个数是( )
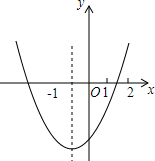 对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:
对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:①abc<0;②16a-4b+c<0;③ax2+bx≥a-b;④3a+c<0.
其中,正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.从六边形的一个顶点作对角线,把这个六边形分成三角形的个数是( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6 个 |
7.点P(4,5)关于x轴对称点的坐标是( )
| A. | (-4,-5) | B. | (-4,5) | C. | (4,-5) | D. | (5,4) |
8. 将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,那么原多边形的边数是( )
将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,那么原多边形的边数是( )
 将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,那么原多边形的边数是( )
将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,那么原多边形的边数是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
 如图,已知△ABC≌△ADE,∠CAE=30°,则∠BAD等于30度.
如图,已知△ABC≌△ADE,∠CAE=30°,则∠BAD等于30度. 已知,如图:AD、BC相交于点O,AD=BC,∠C=∠D=90°.求证:AO=BO,CO=DO.
已知,如图:AD、BC相交于点O,AD=BC,∠C=∠D=90°.求证:AO=BO,CO=DO.