题目内容
17.先化简,再求值:$\frac{x-3}{{x}^{2}-1}$•$\frac{{x}^{2}+2x+1}{x-3}$-($\frac{1}{x-1}$+1),其中x=2cos60°-3.分析 根据分式的乘法和减法可以化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:$\frac{x-3}{{x}^{2}-1}$•$\frac{{x}^{2}+2x+1}{x-3}$-($\frac{1}{x-1}$+1)
=$\frac{x-3}{(x+1)(x-1)}•\frac{(x+1)^{2}}{x-3}-\frac{1+x-1}{x-1}$
=$\frac{x+1}{x-1}-\frac{x}{x-1}$
=$\frac{1}{x-1}$,
当x=2cos60°-3=2×$\frac{1}{2}$-3=1-3=-2时,原式=$\frac{1}{-2-1}=-\frac{1}{3}$.
点评 本题考查分式的化简求值、特殊角的三角函数值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
7.盒中有x枚黑色棋子和y枚白色棋子,这些棋子除颜色外无其他差别.若从盒中随机取出一枚棋子,则它是黑色棋子的概率是$\frac{3}{8}$;若往盒中再放进10枚黑色棋子,则取得黑色棋子的概率变为$\frac{1}{2}$,则x+y的值是( )
| A. | 38 | B. | 40 | C. | 42 | D. | 30 |
8. 如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
 如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )| A. | 43° | B. | 35° | C. | 34° | D. | 44° |
5.-2017的绝对值是( )
| A. | -2017 | B. | -$\frac{1}{2017}$ | C. | 2017 | D. | $\frac{1}{2017}$ |
2.在2,-3,0,-1这四个数中,最小的数是( )
| A. | 2 | B. | -3 | C. | 0 | D. | -1 |
9.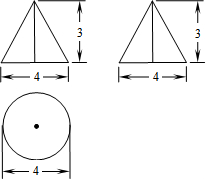 如图是一个几何体的三视图,则该几何体的侧面积是( )
如图是一个几何体的三视图,则该几何体的侧面积是( )
 如图是一个几何体的三视图,则该几何体的侧面积是( )
如图是一个几何体的三视图,则该几何体的侧面积是( )| A. | $2\sqrt{13}π$ | B. | 10π | C. | 20π | D. | $4\sqrt{13}π$ |
6. 如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
 如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |