题目内容
7. 如图,平行四边形ABCD中,AD=2,E在AD边上,BE=2.8,CF⊥CE交BE于F,若∠CED=3∠BEC,则线段BF的长为1.2.
如图,平行四边形ABCD中,AD=2,E在AD边上,BE=2.8,CF⊥CE交BE于F,若∠CED=3∠BEC,则线段BF的长为1.2.
分析 设∠BEC=α,∠BCE=3α,取EF中点G,连接CG,由直角三角形的性质:斜边上的中线等于斜边的一半可得CG=GE=GF,所以∠GCE=∠GEC,进而∠BCG=3α-α=2α=∠GCE+∠GEC=∠BGC,由此可推出BG=BC=2,GF=CG=GE=2.8-2=0.8,BF的长即可求出.
解答 解∵四边形ABCD是平行四边形,
∴AD∥BC, AD=BC=2,
AD=BC=2,
∵∠CED=3∠BEC,
∴∠BCE=∠CED=3∠BEC,
设∠BEC=α,∠BCE=3α,
取EF中点G,连接CG,
∵CF⊥CE交BE于F,
∴∠FCE=90°,
∴CG=GE=GF,
∴∠GCE=∠GEC,
∴∠BCG=3α-α=2α=∠GCE+∠GEC=∠BGC,
∴BG=BC=2,GF=CG=GE=2.8-2=0.8,
∴BF=BG-FG=2-0.8,
故答案为:1.2.
点评 本题考查了平行四边形的性质、直角三角形的性质以及平行线的性质,题目的综合性较强,难度中等,解题的关键是经过层层推理得到BG=BC=2.

练习册系列答案
相关题目
15.下列几何体中左视图是矩形的共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.若代数式$\frac{x-2}{x+2}$的值为0,则x等于( )
| A. | 2 | B. | -2 | C. | 0 | D. | 2,-2 |
12.下列选项中,可以用来证明命题“若|a-1|>1,则a>2”是假命题的反例是( )
| A. | a=2 | B. | a=1 | C. | a=0 | D. | a=-1 |
16.某班的9名学生的体重分别是(单位:千克):70,67,65,63,61,59,59,57,59,这组数据的众数和中位数是( )
| A. | 59,61 | B. | 59,63 | C. | 59,65 | D. | 57,61 |
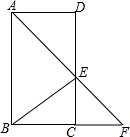 如图,在?ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.
如图,在?ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.
 如图,已知△ABC≌△A′B′C′,AD,A′D′分别是∠BAC和∠B′A′C′的角平分线,试说明AD=A′D′的理由.
如图,已知△ABC≌△A′B′C′,AD,A′D′分别是∠BAC和∠B′A′C′的角平分线,试说明AD=A′D′的理由. 如图,AB是⊙O的直径,C是弧AB的中点,连接AC并延长至D,使DC=CA,连接DB,点E为OB的中点,连接CE并延长交DB的延长线于点F,连接AF交⊙O于点H,连接BH.
如图,AB是⊙O的直径,C是弧AB的中点,连接AC并延长至D,使DC=CA,连接DB,点E为OB的中点,连接CE并延长交DB的延长线于点F,连接AF交⊙O于点H,连接BH.