Question

在△ABC中，CA＝CB，在△AED中， DA＝DE，点D、E分别在CA、AB上，．

（1）如图①，若∠ACB＝∠ADE＝90°，则CD与BE的数量关系是     ；

（2）若∠ACB＝∠ADE＝120°，将△AED绕点A旋转至如图②所示的位置，则CD与BE的数量关系是     ；，

（3）若∠ACB＝∠ADE＝2α（0°< α < 90°），将△AED绕点A旋转至如图③所示的位置，探究线段CD与BE的数量关系，并加以证明(用含α的式子表示)．

 

Answer 1

解：（1）BE＝CD； 

   （2）BE＝CD；  

（3）BE=2CD·sinα．   

证明：如图，分别过点C、D作CM⊥AB于点M，DN⊥AE于点N，

∵ CA＝CB，DA＝DE，∠ACB＝∠ADE=2α ，

∴ ∠CAB＝∠DAE，∠ACM＝∠ADN=α ，AM=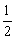AB，AN=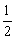AE．

∴∠CAD＝∠BAE．   

Rt△ACM和Rt△ADN中,

sin∠ACM=，sin∠ADN=．

∴ ．

∴ ．

    又 ∵∠CAD＝∠BAE，

∴ △BAE∽△CAD．

∴

∴ BE=2DC·sinα．