题目内容
17.若m为实数(m≠0),且m-$\frac{1}{m}$=4,则m2-$\frac{1}{{m}^{2}}$=±8$\sqrt{5}$.分析 把已知等式两边平方,利用完全平方公式化简,整理求出m2+$\frac{1}{{m}^{2}}$的值,进而求出(m+$\frac{1}{m}$)2的值,开方求出m+$\frac{1}{m}$的值,原式利用平方差公式变形,将各自的值代入计算即可求出值.
解答 解:把m-$\frac{1}{m}$=4,两边平方得:(m-$\frac{1}{m}$)2=m2+$\frac{1}{{m}^{2}}$-2=16,
∴m2+$\frac{1}{{m}^{2}}$=18,即(m+$\frac{1}{m}$)2=m2+$\frac{1}{{m}^{2}}$+2=20,
∴m+$\frac{1}{m}$=±2$\sqrt{5}$,
则原式=(m+$\frac{1}{m}$)(m-$\frac{1}{m}$)=±8$\sqrt{5}$.
点评 此题考查了完全平方公式,以及平方差公式,熟练掌握公式是解本题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
4.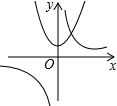 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )| A. | x>1 | B. | x<-1 | C. | 0<x<1 | D. | -1<x<0 |
 如图,把三角形纸片ABC沿DE折叠,使点A落在四边形BCED的内部,已知∠1+∠2=80°,则∠A的度数为40°.
如图,把三角形纸片ABC沿DE折叠,使点A落在四边形BCED的内部,已知∠1+∠2=80°,则∠A的度数为40°.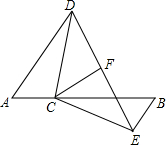 如图,点C在线段AB上,AD∥BE,AC=BE,AD=BC,CF平分∠DCE,
如图,点C在线段AB上,AD∥BE,AC=BE,AD=BC,CF平分∠DCE,