题目内容
已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第4个图形中直角三角形的个数有 个;第2014个图形中直角三角形的个数有 个.
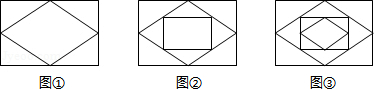

考点:中点四边形
专题:规律型
分析:观察图形可知,两个图形为一个组,直角三角形的个数相同,且都是4的倍数,然后求出第2013个图形的组数,计算即可得解.
解答:解:图①、图②的直角三角形的个数相同,都是4,4=4×1,
图③、图④的直角三角形的个数相同,都是8,8=4×2,
…,
图2013、图2014的直角三角形的个数相同,都是4×
=4028.
故答案为:8;4028.
图③、图④的直角三角形的个数相同,都是8,8=4×2,
…,
图2013、图2014的直角三角形的个数相同,都是4×
| 2014 |
| 2 |
故答案为:8;4028.
点评:本题是对图形变化规律的考查,观察图形,得到两个图形的直角三角形的个数相同是解题的关键.

练习册系列答案
相关题目
小彬在做数学题时,发现下面有趣的结果:
3-2=1
8+7-6-5=4
15+14+13-12-11-10=9
24+23+22+21-20-19-18-17=16
…
根据以上规律可知第99行左起第一个数是 .
3-2=1
8+7-6-5=4
15+14+13-12-11-10=9
24+23+22+21-20-19-18-17=16
…
根据以上规律可知第99行左起第一个数是
已知关于x的二元一次方程组
,若x+y>3,则m的取值范围是( )
|
| A、m>1 | B、m<2 |
| C、m>3 | D、m>5 |
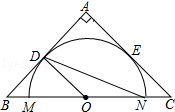 如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则∠MND的度数为
如图,在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则∠MND的度数为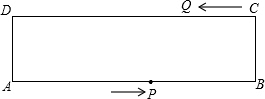 如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过
如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过 如图,半圆O的直径AE=4,弦AB=BC,弦CD=DE,连结OB,OD,则图中两个阴影部分的面积和为
如图,半圆O的直径AE=4,弦AB=BC,弦CD=DE,连结OB,OD,则图中两个阴影部分的面积和为 如图,在△ABC中,AB=AC=7,BC=2,点Q是BC的延长线上一点,且AQ=BQ+CQ,求tanQ=
如图,在△ABC中,AB=AC=7,BC=2,点Q是BC的延长线上一点,且AQ=BQ+CQ,求tanQ=