题目内容
19.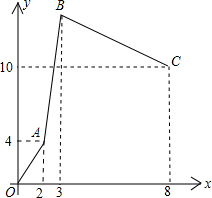 某仓库甲、乙、丙三辆运货车,每辆车只负责进货或出货,每小时的运输量丙车最多,乙车最少,乙车的运输量为每小时6吨,下图是从早晨上班开始库存量y(吨)与时间x(小时)的函数图象,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙工作.
某仓库甲、乙、丙三辆运货车,每辆车只负责进货或出货,每小时的运输量丙车最多,乙车最少,乙车的运输量为每小时6吨,下图是从早晨上班开始库存量y(吨)与时间x(小时)的函数图象,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙工作.(1)甲、乙、丙三辆车中,谁是进货车?
(2)甲车和丙车每小时各运输多少吨?
(3)由于仓库接到临时通知,要求三车在8小时后同时开始工作,但丙车在运送10吨货物后出现故障而退出,问:8小时后,甲、乙两车又工作了几小时,使仓库的库存量为6吨.
分析 (1)由BC段库存减少结合此时只有甲、乙工作且乙车运货量最少,可知甲车为出货车;由B、C点坐标结合乙车的运输量为每小时6吨,可得知乙车为进货车;由OA段库存增加,且OA段只有甲、丙车工作,可知丙车为进货车;
(2)设甲车每小时运货x吨,丙车每小时运货y吨,结合图形中各点的坐标可列出关于x、y的二元一次方程组,解方程组即可得出结论;
(3)设8小时后,甲、乙两车又工作了t小时,库存量是6吨,由库存=原库存+进货量-出货量,可列出关于t的一元一次方程,解方程即可得出结论.
解答 解:(1)∵每小时的运输量丙车最多,乙车最少,BC段只有甲、乙工作,且库存在减少,
∴甲车是出货车,
又∵OA段只有甲、丙车工作,库存在增加,
∴丙车是进货车,
∵结合B、C点的坐标,且乙车的运输量为每小时6吨,
可知乙车为进货车.
故乙、丙车是进货车,甲车是出货车.
(2)设甲车每小时运货x吨,丙车每小时运货y吨,
由已知得:$\left\{\begin{array}{l}{2(y-x)=4}\\{(6+y)+(8-3)(6-x)=10-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$.
故甲车每小时运输8吨货物,丙车每小时运输10吨货物.
(3)设8小时后,甲、乙两车又工作了t小时,库存量是6吨,
则有(-8+6)t+10+10=6,
解得:t=7.
答:8小时后,甲、乙两车又工作了7小时,库存量是6吨.
点评 本题考查了一次函数的性质、二元一次方程组的应用以及一元一次方程的应用,解题的关键:(1)结合图形得出结论;(2)根据图形中的点的坐标列出关于x、y的二元一次方程组;(3)根据数量关系列出关于t的一元一次方程.本题属于中档题,难度不大,解决该题型题目时利用数形结合列出方程(或方程组),解方程(或方程组)即可得出结论.

| A. | 3(x-1)-2(2x+3)=6 | B. | 3x-3-4x+3=1 | C. | 3(x-1)-2(2x+3)=1 | D. | 3x-3-4x-2=6 |
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
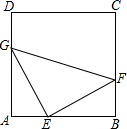 如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF.
如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF. 如图,AC丄BC,AC=9cm,BC=12cm,AB=15cm,点C到直线AB的距离是为$\frac{36}{5}$cm.
如图,AC丄BC,AC=9cm,BC=12cm,AB=15cm,点C到直线AB的距离是为$\frac{36}{5}$cm.