题目内容
8.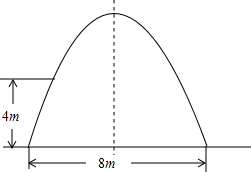 如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )
如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )| A. | 6.0m | B. | 5.3m | C. | 5.6m | D. | 5.9m |
分析 建立坐标系,抛物线的顶点坐标为(0,9),设抛物线解析式为y=ax2+9,又知抛物线过(4,0),可求出a.把y=4代入函数表达式即可解决问题.
解答 解:如图,抛物线的顶点坐标为(0,9),
设抛物线解析式为y=ax2+9,
又知抛物线过(4,0),
∴0=16a+9,
解得:a=-$\frac{9}{16}$,
∴y=-$\frac{9}{16}$x2+9,
把y=4代入y=-$\frac{9}{16}$x2+9,
解得:x=±$\frac{4\sqrt{5}}{3}$,
故两壁灯之间水平距离为$\frac{8\sqrt{5}}{3}$≈5.96≈6.0.
故选A.
点评 本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
 如图,在等边△CDE中,A、B分别是ED、DE延长线上的点,且DE2=AD•EB,求∠ACB的度数.
如图,在等边△CDE中,A、B分别是ED、DE延长线上的点,且DE2=AD•EB,求∠ACB的度数.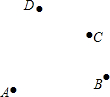 如图,平面上有A、B、C、D4个点,根据下列语句画图.
如图,平面上有A、B、C、D4个点,根据下列语句画图.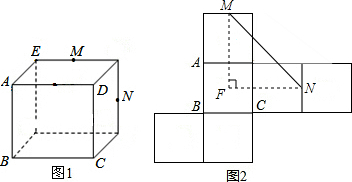
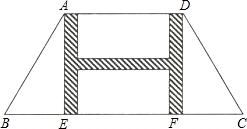 如图,有一块等腰梯形的草坪,草坪上底AD长48m,下底BC长108m,上下底之间的距离AE(或DF)是40m.现要在草坪中修建横、纵向的“H”型甬道,甬道宽度相等,设甬道的宽为x m.
如图,有一块等腰梯形的草坪,草坪上底AD长48m,下底BC长108m,上下底之间的距离AE(或DF)是40m.现要在草坪中修建横、纵向的“H”型甬道,甬道宽度相等,设甬道的宽为x m. 请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.
请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.