Question

如图所示，点D在⊙O的直径AB的延长线上，点C在⊙O上，且AC=CD，∠ACD=120°．

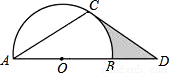
（1）求证：CD是⊙O的切线；

（2）若⊙O的半径为2，求圆中阴影部分的面积.

 

Answer 1

【答案】

（1）证明见解析；（2）．

【解析】

试题分析：（1）连接OC，根据等腰三角形的性质，三角形的内角和与外角的性质，证得∠OCD=90°，即可证得CD是⊙O的切线；

(2)由（1）知△OCD是直角三角形，因此阴影部分的面积等于Rt△OCD的面积-扇形OCB的面积，分别求出它们的面积即可得出结果.

试题解析：（1）证明：连接OC，

∵CA=CD，∠ACD=120°，

∴∠A=∠D=30°，

∴∠COD=2∠A=2×30°=60°，

∴∠OCD=180°-60°-30°=90°，

∴OC⊥CD，

∵OC是⊙O的半径，

∴CD是⊙O的切线；

（2）解：∵∠A=30°，

∴∠1=2∠A=60°．

∴S_扇形OBC=．

在Rt△OCD中，∵，

∴．

∴．

∴图中阴影部分的面积为．

考点: （1）切线的判定；（2）扇形的面积.