题目内容
10.解方程:(1)x2+2x-8=0;
(2)2x2+4x-1=0;
(3)(x-1)(x+3)=12;
(4)(x-1)2=(2x+3)2.
分析 (1)方程利用因式分解法求出解即可;
(2)方程利用公式法求出解即可;
(3)方程整理后,利用因式分解法求出解即可;
(4)方程利用两数的平方相等,两数相等或互为相反数求出解即可.
解答 解:(1)分解因式得:(x-2)(x+4)=0,
可得x-2=0或x+4=0,
解得:x=2或x=-4;
(2)这里a=2,b=4,c=-1,
∵△=16+8=24,
∴x=$\frac{-4±2\sqrt{6}}{4}$=$\frac{-2±\sqrt{6}}{2}$;
(3)方程整理得:x2+2x-15=0,
分解因式得:(x-3)(x+5)=0,
可得x-3=0或x+5=0,
解得:x=3或x=-5;
(4)开方得:x-1=2x+3或x-1=-2x-3,
解得:x=-4或x=-$\frac{2}{3}$.
点评 此题考查了解一元二次方程-因式分解法,公式法,以及直接开平方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.三边长均为整数且周长为12的三角形的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
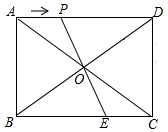 如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s.
如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s. 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF. 如图,在△ABC中,AB=AC,D为AC上的一点,求证:AC>$\frac{1}{2}$(BD+CD).
如图,在△ABC中,AB=AC,D为AC上的一点,求证:AC>$\frac{1}{2}$(BD+CD).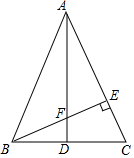 如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?
如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?