��Ŀ����
����������12�֣���ͼ�����κ���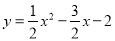 ��ͼ����x�ύ�ڵ�A��B����M��N��x���ϣ���N�ڵ�M�Ҳ࣬MN��2����MNΪֱ�DZ�����������ֱ��������CMN����CMN��90�㣮���M�ĺ�����Ϊm��
��ͼ����x�ύ�ڵ�A��B����M��N��x���ϣ���N�ڵ�M�Ҳ࣬MN��2����MNΪֱ�DZ�����������ֱ��������CMN����CMN��90�㣮���M�ĺ�����Ϊm��
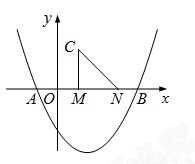
��1������C��������������ʱ����m��ֵ��
��2�����߶�CN�Ƶ�N��ʱ����ת90��õ���Ӧ�߶�DN��
�ٵ���D�����������ߵĶԳ�����ʱ�����D�����꣮
����DNΪֱ�DZ�������ֱ��������DNE������E�����������ߵĶԳ�����ʱ����m��ֵ��
��1��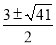 ����2���٣�
����2���٣�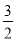 ����2������
����2������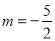 ��
��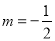 ��
��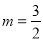 ��
��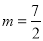 ��
��
��������
�����������1���ȸ��ݵ���ֱ�������ε����������C������Ϊ��m��2�����ٽ�C��������� ���������m��ֵ��
���������m��ֵ��
��2����������ת�����ʵó���D������Ϊ��m����2�����ٸ��ݶ��κ������������������ �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ�� ��Ȼ����ݵ�D��ֱ��
��Ȼ����ݵ�D��ֱ�� �ϣ����������D�����ꣻ
�ϣ����������D�����ꣻ
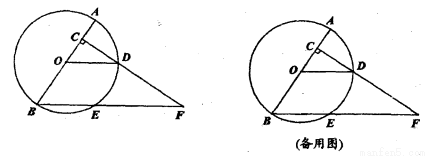
����DNΪֱ�DZ�������ֱ��������DNEʱ���ֱ���D��NΪֱ�Ƕ��㣬��DN������ֱ���������ֱ��������DNE��E���λ�÷�����������ۣ����ÿһ��������������ȸ��ݵ���ֱ�������ε����������E�����꣬Ȼ����ݵ�E��ֱ�� �ϣ��г�����m�ķ��̣��ⷽ�̼������m��ֵ��
�ϣ��г�����m�ķ��̣��ⷽ�̼������m��ֵ��
�����������1���ߡ�CMN�ǵ���ֱ��������CMN����CMN=90�㣬��CM=MN=2�����C������Ϊ��m��2�����ߵ�C��m��2�����������ϣ���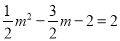 �����
�����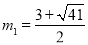 ��
��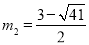 �����C��������������ʱ��m��ֵΪ
�����C��������������ʱ��m��ֵΪ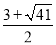 ��
��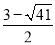 ��
��
��2���١߽��߶�CN�Ƶ�N��ʱ����ת90��õ���Ӧ�߶�DN�����CND=90�㣬DN=CN=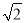 CM=
CM=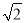 MN����CD=
MN����CD=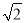 CN=2CM=2MN����DM=CM=MN����DMN=90�㣬���D������Ϊ��m����2�����֡�������
CN=2CM=2MN����DM=CM=MN����DMN=90�㣬���D������Ϊ��m����2�����֡������� �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ�� ����D�����������ߵĶԳ����ϣ����D������Ϊ��
����D�����������ߵĶԳ����ϣ����D������Ϊ��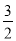 ����2����
����2����
����ͼ����DNΪֱ�DZ�������ֱ��������DNE��E���λ����������������E����E1��λ��ʱ���ߵ�D������Ϊ��m����2����MN=ME1=2����N������Ϊ��m+2��0�������E1�ģ�m��2��0�����ߵ�E1�������� �ĶԳ���ֱ��
�ĶԳ���ֱ�� �ϣ���
�ϣ���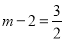 �����
�����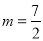 ��
��
���E����E2��λ��ʱ���ߵ�D������Ϊ��m����2������N������Ϊ��m+2��0�������E2�ģ�m+2����4�����ߵ�E2�������� �ĶԳ���ֱ��
�ĶԳ���ֱ�� �ϣ���
�ϣ���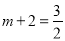 �����
����� ��
��
���E����E3��λ��ʱ���ߵ�D������Ϊ��m����2�������E3�ģ�m��2�����ߵ�E3�������� �ĶԳ���ֱ��
�ĶԳ���ֱ�� �ϣ���
�ϣ���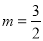 ��
��
���E����E4��λ��ʱ���ߵ�D������Ϊ��m����2������N������Ϊ��m+2��0�������E4�ģ�m+4����2�����ߵ�E4�������� �ĶԳ���ֱ��
�ĶԳ���ֱ�� �ϣ���
�ϣ���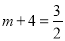 �����
�����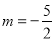 ��
��
���Ͽ�֪������E�����������ߵĶԳ�����ʱ�����з���������m��ֵΪ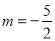 ��
��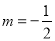 ��
��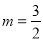 ��
��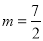 ��
��
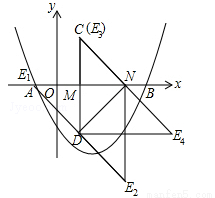
���㣺���κ����ۺ��⣮

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�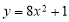 B��
B��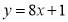 C��
C��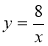 D��
D��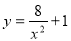



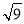 ��ƽ������
��ƽ������