题目内容
如图,已知AB是⊙O的直径,AB=8,点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,连结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F.
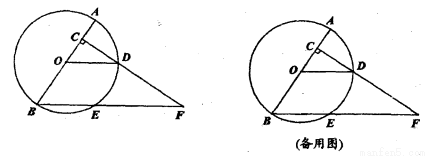
(1)若ED=BE,求∠F的度数:
(2)设线段OC=a,求线段BE和EF的长(用含a的代数式表示);
(3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长.
(1)30°;(2)EF= ;(3)CO的长为
;(3)CO的长为 或
或 时,△PEB为等腰三角形.
时,△PEB为等腰三角形.
【解析】
试题分析:(1)利用圆周角定理以及三角形内角和定理得出即可;
(2)首先证明△HBO≌△COD(AAS),进而利用△COD∽△CBF,得出比例式求出EF的长;
(3)分别利用①当PB=PE,不合题意舍去;②当BE=EP,③当BE=BP,求出即可.
试题解析:(1)如图1,连接EO,

∵
∴∠BOE=∠EOD,
∵DO∥BF,
∴∠DOE=∠BEO,
∵BO=EO,
∴∠OBE=∠OEB,
∴∠OBE=∠OEB=∠BOE=60°,
∵CF⊥AB,
∴∠FCB=90°,
∴∠F=30°;
(2)如图1,作HO⊥BE,垂足为H,
∵在△HBO和△COD中
 ,
,
∴△HBO≌△COD(AAS),
∴CO=BH=a,
∴BE=2a,
∵DO∥BF,
∴△COD∽△CBF,
∴
∴ ,
,
∴EF= ;
;
(3)∵∠COD=∠OBE,∠OBE=∠OEB,∠DOE=∠OEB,
∴∠COD=∠DOE,
∴C关于直线OD的对称点为P在线段OE上,
若△PEB为等腰三角形,设CO=x,∴OP=OC=x,则PE=EO-OP=4-x,
由(2)得:BE=2x,
①当PB=PE,不合题意舍去;
②当BE=EP,2x=4-x,解得:x= ,
,
③当BE=BP,作BM⊥EO,垂足为M,

∴EM= PE=
PE= ,
,
∴∠OEB=∠COD,∠BME=∠DCO=90°,
∴△BEM∽△DOC,
∴ ,
,
∴ ,
,
整理得:x2+x-4=0,
解得:x= (负数舍去),
(负数舍去),
综上所述:当CO的长为 或
或 时,△PEB为等腰三角形.
时,△PEB为等腰三角形.
考点:圆的综合题.

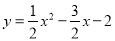 的图像与x轴交于点A,B.点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.
的图像与x轴交于点A,B.点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.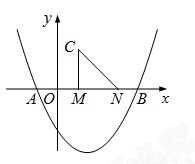
 .
.