题目内容
16.计算:(1)(x+3)2+x(x-6)
(2)(x+1-$\frac{x+{x}^{2}}{x-1}$)÷$\frac{{x}^{3}+{x}^{2}}{{x}^{2}-2x+1}$.
分析 (1)首先利用完全平方公式以及单项式与多项式乘法法则计算,然后合并同类项即可求解;
(2)首先对括号内的式子通分相减,把除法转化为乘法,然后进行约分即可.
解答 解:(1)原式=x2+6x+9+x2-6x=2x2+9;
(2)原式=$\frac{(x+1)(x-1)-(x+{x}^{2})}{x-1}$÷$\frac{{x}^{2}(x+1)}{(x-1)^{2}}$
=$\frac{{x}^{2}-1-x-{x}^{2}}{x-1}$÷$\frac{{x}^{3}+{x}^{2}}{(x-1)^{2}}$
=$\frac{-(x+1)(x-1)}{(x-1)^{2}}$÷$\frac{{x}^{3}+{x}^{2}}{(x-1)^{2}}$
=-$\frac{x+1}{x-1}$•$\frac{(x-1)^{2}}{{x}^{2}(x+1)}$
=-$\frac{x-1}{{x}^{2}}$.
点评 本题考查整式的混合运算和分式的混合运算,正确进行分解因式是关键.

练习册系列答案
相关题目
 如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.
如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.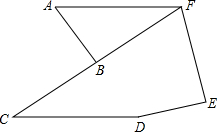 如图,已知AB=DE,BC=EF,CD=FA,∠ABC=86°,∠E=86°,求证:AF∥CD.
如图,已知AB=DE,BC=EF,CD=FA,∠ABC=86°,∠E=86°,求证:AF∥CD.