题目内容

某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元．为了扩大销售，商场决定采取适当的降价措施，经调查发现，如果每件衬衫降价1元，商场平均每天可多售出2件．

（1）若使商场平均每天赢利1200元，则每件衬衫应降价多少元？

（2）若想获得最大利润，每件衬衫应降价多少元？最大利润为多少元？

（1）应降价10元或20元；（2）15元，最大利润1250元． 【解析】试题分析：（1）设每件衬衫应降价x元，根据每件的利润×销售量=平均每天的盈利，列方程求解即可； （2）根据：总利润=单件利润×销售量列出函数关系式，配方成二次函数顶点式可得函数最值情况． 试题解析：（1）设每件衬衫应降价x元， 则依题意，得：（40﹣x）（20+2x）=1200， 整理，得，﹣2x...
练习册系列答案
相关题目

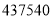用四舍五入法对取近似数，精确到千位为__________．（用科学记数法表示）

【解析】精确到千位为，用科学记数法表示为． 故答案为： .

下列计算正确的是（ ）

A. 3a+2b=5ab B. 5y-3y=2 C. 7a+a=7a2 D. 3x2y-2yx2=x2y

D 【解析】试题分析：依据合并同类项法则进行计算即可． 【解析】 A、3a与2b不是同类项，不能合并，故A错误； B、5y﹣3y=2y，故B错误； C、7a+a=8a，故C错误； D、6xy2﹣3y2x=3xy2，故D正确． 故选：D．

分解因式： =_________.

【解析】试题解析：原式 故答案为：

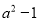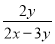如果把中的x和y都扩大5倍，那么分式的值（ ）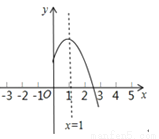

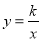A. 不变 B. 扩大5倍 C. 缩小5倍 D. 扩大4倍

A 【解析】试题解析： 分式的值不变. 故选A.

二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的对称轴是直线x=1，其图象的一部分如图所示，对于下列说法：①abc＜0；②a﹣b+c＜0；③3a+c＜0；④当﹣1＜x＜3时，y＞0．其中正确的是______（把正确说法的序号都填上）

①②③． 【解析】∵抛物线的开口向下，∴a<0. ∴－>0，∴<0， ∴b>0，令x＝0，则y＝c>0， ∴abc<0，所以①正确； ∵对称轴为x＝1，图象与x轴的一个交点位于2、3之间，∴图象与x轴的另一交点位于0、－1之间，∴当x＝－1时，a－b＋c<0，所以②正确； ∵－＝1，∴b＝－2a. ∴y＝ax2＋bx＋c＝ax2－2ax＋c， 当x＝...

如图，反比例函数的图象经过点A（2，1），若y≤1，则x的范围为（　　）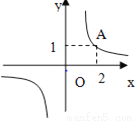

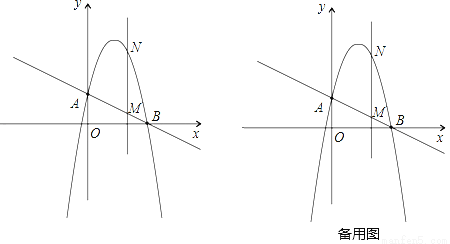
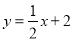A. x≥1 B. x≥2 C. x＜0或0＜x≤1 D. x＜0或x≥2

D 【解析】试题解析：在第一象限纵坐标为1的以及小于1的函数图象所对应的自变量的取值为 在第三象限纵坐标为1的以及小于1的函数图象所对应的自变量的取值为 故选D．

将一根24 cm的筷子，置于底面直径为15 cm，高8 cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度为h cm，则h的取值范围是___________．

7≤h≤16 【解析】试题分析：根据杯子内筷子的长度取值范围得出杯子外面长度的取值范围，即可得出答案． ∵将一根长为24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中， ∴在杯子中筷子最短是等于杯子的高，最长是等于杯子斜边长度， ∴当杯子中筷子最短是等于杯子的高时，x=12， 最长时等于杯子斜边长度是：x==13， ∴h的取值范围是：（24-13）...

如图，一次函数分别交y轴、x轴于A、B两点，抛物线y=﹣x2+bx+c过A、B两点．

（1）求这个抛物线的解析式；

（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？

（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．

（1）y=?x²+x+2；（2）t=2时，MN有最大值4;（3）(0,6),(0,?2)或(4,4)． 【解析】试题分析： （1）先由直线分别交y轴、x轴于点A、B这一条件求出点A、B的坐标，将所求坐标代入抛物线列出关于的值即可得到所求抛物线的解析式； （2）如图1，由题意可知点M的横坐标为t，根据点M在直线上，点N在（1）中所求抛物线上，可用含“t”的代数式表达出点M、N的坐标...

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网