Question

【题目】对于平面直角坐标系中的动点和图形，给出如下定义：如果为图形上一个动点，，两点间距离的最大值为，，两点间距离的最小值为，我们把的值叫点和图形间的“和距离”，记作（，图形）.

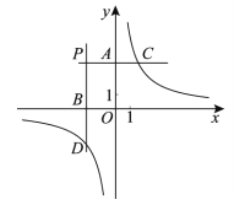
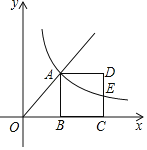
（1）如图，正方形的中心为点，.

①点到线段的“和距离”（，线段）=______；

②设该正方形与轴交于点和，点在线段上，（，正方形）=7，求点的坐标.

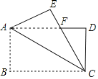
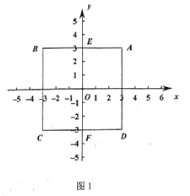
（2）如图2，在（1）的条件下，过，两点作射线，连接，点是射线上的一个动点，如果（，线段），直接写出点横坐标取值范围.

Answer 1

【答案】（1）①；②的坐标为和；（2）.

【解析】

（1）①根据“和距离“的定义计算：OE是两点间距离的最小值，OA是两点间的最大值，相加可得结论；②分两种情况：P在y轴的正半轴和负半轴上，根据“和距离“的定义，并由d（P，正方形ABCD）=7，列方程计算即可；

（2）分M在线段CD上和延长线上两种情况，利用“和距离”的定义列方程可得结论．

（1）①如下图所示，连接OA，

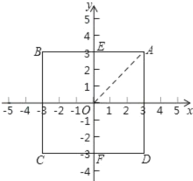
∵四边形ABCD是正方形，且A（3，3），

∴，

∴

即d（O，线段AB）=

故答案为：；

②如下图所示，设，

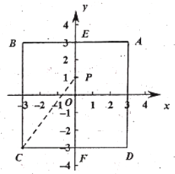
∵点在线段上，

∴.

当时，由题意可知，.

∴，，.

∵（，正方形），

∴.

∴.

在中，由勾股定理得，

解得.

∴.

当时，由对称性可知.

综上，的坐标为和.

（2）分两种情况：

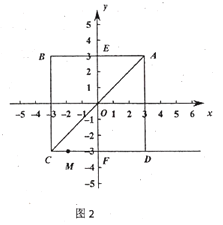
①当-3≤t<3时，如下图所示，M在线段CD上，过M作MN⊥AC于N，连接AM，

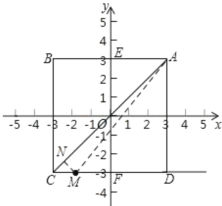
∵M点横坐标是t，

∴CM=t+3，

∵四边形ABCD是正方形，

∴∠ACD=45°，

∴△CMN是等腰直角三角形，

∴MN=CM=，

∴（，线段）=MN+MA=，

②当t≥3时，如下图所示，M在线段CD的延长线上，过M作MN⊥AC于N，

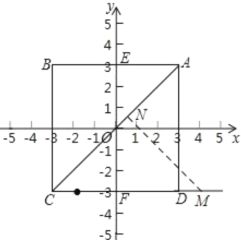
同理可得MN=CM=，

∴（，线段）=MN+CM=，

∵M从C到D方向上运动时，MN+MA越来越大，

∴

解得：，

解得：，

∴点横坐标的取值范围是.