题目内容
【题目】已知正方形
在平面直角坐标系中，点
，
分别在
轴，
轴的正半轴上，等腰直角三角形
的直角顶点
在原点，
，
分别在
，
上，且
，
．将
绕点逆时针旋转，得点，旋转后的对应点为
，
．
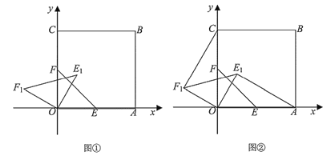
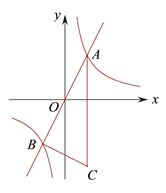
（Ⅰ）①如图①，求
的长；②如图②，连接
，
，求证
；
（Ⅱ）将绕点逆时针旋转一周，当
时，求点的坐标（直接写出结果即可）．
【答案】（Ⅰ）①
；②见解析；（Ⅱ）点
的坐标为
或
．
【解析】
（1）①根据勾股定理求出EF的长，
的长；根据SAS定理证明
即可；
（2）由于△OEF是等腰Rt△，若OE∥CF，那么CF必与OF垂直；在旋转过程中，E、F的轨迹是以O为圆心，OE（或OF）长为半径的圆，若CF⊥OF，那么CF必为⊙O的切线，且切点为F；可过C作⊙O的切线，那么这两个切点都符合F点的要求，因此对应的E点也有两个；在Rt△OFC中，OF=2，OC=OA=4，可证得∠FCO=30°，即∠EOC=30°，已知了OE的长，通过解直角三角形，不难得到E点的坐标，由此得解．
解：（Ⅰ）①∵等腰直角三角形
的直角顶点
在原点，
，
∴
，
．
在
中，由勾股定理，得
．
∵
是由
绕点逆时针旋转得到的，
∴．
②∵四边形
为正方形，
∴
，
∵将绕点逆时针旋转，得，
∴
，
又是等腰直角三角形，
∴是等腰直角三角形，
∴
，
∴．
（Ⅱ）如图，
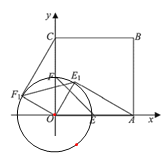
∵OE⊥OF，
∴过点F与OE平行的直线有且只有一条，并与OF垂直，
当三角板OEF绕O点逆时针旋转一周时，
则点F在以O为圆心，以OF为半径的圆上．
∴过点F与OF垂直的直线必是圆O的切线．
又点C是圆O外一点，过点C与圆O相切的直线有且只有2条，不妨设为CF1和CF2，
此时，E点分别在E1点和E2点，满足CF1∥OE1，CF2∥OE2．
当切点F1在第二象限时，点E1在第一象限．
cos∠COF1=
，
∴∠COF1=60°，∴∠AOE1=60°．
∴点E1的横坐标为：xE1=2cos60°=1，
点E1的纵坐标为：yE1=2sin60°=
，
∴点E1的坐标为(1，)；
当切点F2在第一象限时，点E2在第四象限．
同理可求：点E2的坐标为(1，-)．
综上所述，三角板OEF绕O点逆时针旋转一周，存在两个位置，使得OE∥CF，
此时点E的坐标为E1(1，)或E2(1，-)．
