Question

【题目】 如图，四边形ABCD内接于以BC为直径的圆，圆心为O，且AB=AD，延长CB、DA交于P，过C点作PD的垂线交PD的延长线于E，且PB=BO，连接OA．

（1）求证：OA∥CD；

（2）求线段BC：DC的值；

（3）若CD=18，求DE的长．

Answer 1

【答案】（1）详见解析；（2）；（3）DE=．

【解析】

（1）连接BD，由圆周角定理可知∠BDC=90°，即CD⊥BD，再由AB=AD可知，则OA⊥BD，由此即可得出结论；

（2）设⊙O的半径为r，则PB=OB=OC=OA=r，再由OA∥CD可知，△OAP∽△CDP，故可得出=，故可用r表示出CD的长，再求出BC：DC的值即可；

（3）由OF∥CD，OB=OC根据中位线定理可以求出OF，AF；再根据勾股定理在Rt△DBC中可以求出BD，DF；接着在Rt△ADF中求出AD；然后利用平行线的性质得∠FAD=∠CDE证明△AFD∽△DEC，利用相似三角形的对应边成比例可以求出DE．

（1）证明：连接BD，交OA于点F．

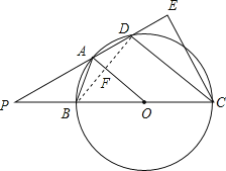
∵BC是⊙O的直径，

∴∠BDC=90°，即CD⊥BD，

∵AB=AD，

∴

∴OA⊥BD，

∴OA∥CD；

（2）解：设⊙O的半径为r，

∵PB=OB，

∴PB=OB=OC=OA=r，

∵OA∥CD，

∴△OAP∽△CDP，

∴=，=，解得CD=，

∴==；

（3）解：∵CD=18, CD=，∴r=12

∵OF∥CD，==，

∴OF=9，AF=3；

∵BD==6，

∴DF=BD=3，

∴AD==6；

∵∠AFD=∠DEC=90°，OA∥DC，∠FAD=∠CDE，

∴△AFD∽△DEC，

∴=，即=；

∴DE=．