Question

【题目】如果抛物线的顶点在抛物线上，同时，抛物线的顶点在抛物线上，那么我们称抛物线与关联.

（1）已知抛物线：与：，请判断抛物线 与抛物线是否关联，并说明理由.

（2）抛物线，动点的坐标为，将抛物线绕点旋转180°得到抛物线，若抛物线与关联，求抛物线的解析式.

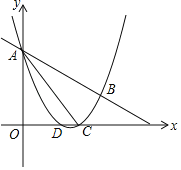
（3）点为抛物线：的顶点，点为抛物线关联的抛物线的顶点，是否存在以为斜边的等腰直角三角形ABC，使其直角顶点在直线上？若存在，求出点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）M在C上，M在C上；（2），；（3）

【解析】

（1）C：顶点坐标M（1，5），当x=1时，y=2x2+4x-1=5，故抛物线C1顶点在C2的抛物线上，即可求解；

（2）求出C2顶点坐标为（9+2t，-2），将该顶点坐标代入C1的函数表达式得：-2=-（9+2t+9）2+6，即可求解；

（3）设点C（-10，n），点B（-1，-2）或（-17，-2），点A（-9，6），以AB为斜边的等腰直角三角形ABC，则AC2=BC2且AC2+BC2=AB2，即可求解．

（1）C：顶点坐标M（1，5），

当x=1时，y=2x2+4x-1=5，故抛物线C1顶点在C2的抛物线上；

C：顶点坐标M（-1，-3），

同理可得：抛物线C2顶点在C1的抛物线上，

故：抛物线C1与抛物线C2相互关联；

（2）C1抛物线顶点坐标为：（-9，6），点P的坐标为（t，2），

由中点公式得：C2顶点坐标为（9+2t，-2），

将该顶点坐标代入C1的函数表达式得：-2=-（9+2t+9）2+6，

解得：t=-5或-13，

故C2顶点坐标为（-1，-2）或（-17，-2），

故函数C2的表达式为：y＝ (x+1)22或y＝ (x+17)22；

（3）存在，理由：

设点C（-10，n），点A（-9，6），

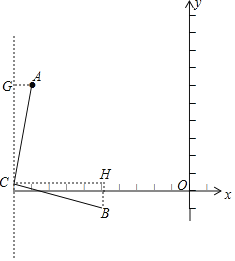
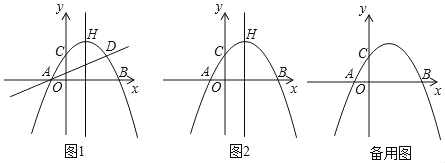
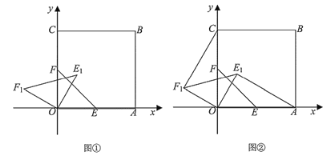
当点B在函数对称轴的右侧时，如图，∠ACB=90°，CA=CB，

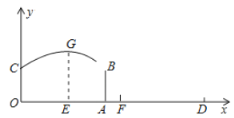
作直线l：x=-10，过点A作直线l的垂线交于点G，

过点C作x轴的平行线、过点B作x轴的垂线，两条直线交于点H，

∵∠GCA+∠AGH=90°，∠AGH+∠BCH=90°，

∴∠BCH=∠ACG，

∠CGA=∠CHB=90°，CA=CB，

∴△CGA≌△CHB（AAS），

∴BH=AG，CG=CH，

则点B（-4-n，n-1），

将点B的坐标代入抛物线C1：y＝ (x+9)+6并解得：n=1±4；

综上，点C的坐标为：（-10，1+4）或（-10，1-4）．

当点B在函数对称轴的左侧时，

同理可得点B（n-16，n+1），

将点B的坐标代入函数表达式并解得：n=3，

综上，点C的坐标为：（-10，1+4）或（-10，1-4）或（-10，3）．