题目内容
13.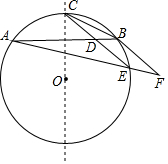 如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1:$\sqrt{5}$,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
分析 ①连接AC,BE,由等腰三角形的性质和三角形的外角性质得出∠F=$\frac{1}{2}$∠AEB,由圆周角定理得出∠AEC=∠BEC,证出∠AEC=∠F,即可得出结论;
②证明△ADE∽△CBE,得出$\frac{AD}{CB}=\frac{3}{\sqrt{5}}$,证明△CBE∽△CDB,得出$\frac{BD}{CB}=\frac{BE}{CE}$,求出CB=2$\sqrt{5}$,得出AD=6,AB=8,由垂径定理得出OC⊥AB,AG=BG=$\frac{1}{2}$AB=4,由勾股定理求出CG=$\sqrt{C{B}^{2}-B{G}^{2}}$=2,即可得出△BCD的面积.
解答 ①证明:连接AC,BE,作直线OC交AB于G,如图所示:
∵BE=EF,
∴∠F=∠EBF;
∵∠AEB=∠EBF+∠F,
∴∠F=$\frac{1}{2}$∠AEB,
∵C是$\widehat{AB}$的中点,∴$\widehat{AC}=\widehat{BC}$,
∴∠AEC=∠BEC,
∵∠AEB=∠AEC+∠BEC,
∴∠AEC=$\frac{1}{2}$∠AEB,
∴∠AEC=∠F,
∴CE∥BF;
②解:∵∠DAE=∠DCB,∠AED=∠CEB,
∴△ADE∽△CBE,
∴$\frac{AD}{CB}=\frac{AE}{CE}$,即$\frac{AD}{CB}=\frac{3}{\sqrt{5}}$,
∵∠CBD=∠CEB,∠BCD=∠ECB,
∴△CBE∽△CDB,
∴$\frac{BD}{CB}=\frac{BE}{CE}$,即$\frac{2}{CB}=\frac{1}{\sqrt{5}}$,
∴CB=2$\sqrt{5}$,
∴AD=6,
∴AB=8,
∵点C为劣弧AB的中点,
∴OC⊥AB,AG=BG=$\frac{1}{2}$AB=4,
∴CG=$\sqrt{C{B}^{2}-B{G}^{2}}$=2,
∴△BCD的面积=$\frac{1}{2}$BD•CG=$\frac{1}{2}$×2×2=2.
点评 本题考查了相似三角形的判定与性质、垂径定理、圆周角定理、三角形的外角性质、勾股定理等知识;熟练掌握圆周角定理和垂径定理,证明三角形相似是解决问题的关键.

| A. | x2+8x+16 | B. | x2+8x+8 | C. | x2+16 | D. | x2-4x+16 |
 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F. 如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.
如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.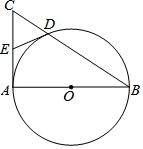 如图,在Rt△ABC中,∠CAB=90°,以AB为直径的⊙O交BC于点D,点E是AC的中点,连接DE.
如图,在Rt△ABC中,∠CAB=90°,以AB为直径的⊙O交BC于点D,点E是AC的中点,连接DE. 某电脑公司现有A、B、C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
某电脑公司现有A、B、C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.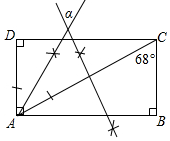 如图,依据尺规作图的痕迹,计算∠α=56°.
如图,依据尺规作图的痕迹,计算∠α=56°.