��Ŀ����
5����ͼ1������ABCD�У���֪��BAD=120�㣬��EGF=60�㣬��EGF�Ķ���G�����ζԽ���AC���˶����ǵ����߷ֱ�BC��CD�ڵ�E��F��$\frac{AC}{CG}$=t����1����ͼ2��������G�˶������A�غ�ʱ����֤��EC+CF=BC��
��2��֪ʶ̽����
����ͼ3��������G�˶���AC�е�ʱ��̽���߶�EC��CF��BC��������ϵ��
���ڶ���G���˶������У���ֱ��д���߶�EC��CF��BC��������ϵ������Ҫд��֤�����̣���
��3����������
��ͼ4����֪���α߳�Ϊ8��BG=7��CF=$\frac{6}{5}$����t��2ʱ����EC�ij��ȣ�

���� ��1����ͼ2�У���CA��ȡһ��M��ʹ��CM=CE������EM������֤����ABE�ա�ACF����֤����AEM�ա�FEC�����ɽ�����⣮
��2���ٽ��ۣ�EC+CF=$\frac{1}{2}$BC����ͼ3�У�ȡBC�е�P��CD�е�Q������PG��GQ�����ã�1���Ľ��۽�����⣮
�ڽ��ۣ�CE+CF=$\frac{BC}{t}$����ͼ4�У���GP��AB��BC��P��GQ��AD��CD��Q�����ã�1���Ľ��۽�����⣮
��3����ͼ4�У���BM��AC��M�����ã�1���Ľ��ۣ�CG=CE+CF�����CE���ɽ�����⣮
��� ��1��֤��������һ����ͼ2�У���CA��ȡһ��M��ʹ��CM=CE������EM��
���ı���ABCD�����Σ���BAD=120�㣬
��AB=BC=CD=AD����CAB=��CAD=60�㣬
���ABC����ACD���ǵȱ������Σ�
���AB=AC����BAC=��EAF=60�㣬��B=��ACF=60�㣬
���BAE=��CAF��
�ڡ�BAE�͡�CAF�У�
$\left\{\begin{array}{l}{��BAE=��CAF}\\{��B=��ACF}\\{AB=AC}\end{array}\right.$��
���ABE�ա�ACF��
��AE=AF���ߡ�EAF=60�㣬
���AEF�ǵȱ������Σ�
��CE=CM����ECM=60�㣬
���ECM�ǵȱ������Σ�
���AEF=��MEC=60�㣬AE=EF��EM=EC��
���AEM=��FEC��
�ڡ�AEM�͡�FEC�У�
$\left\{\begin{array}{l}{AE=EF}\\{��AEM=��FEC}\\{EM=EC}\end{array}\right.$��
���AEM�ա�FEC��
��AM=CF��
��BC=AC=AM+CM=EC+CF��
��������ֻҪ֤����ABE�ա�ACF�������Ƴ�BE=CF���Ƴ�AC=BC=BE+CE=CF+CE��
��2���ٽ��ۣ�EC+CF=$\frac{1}{2}$BC��
���ɣ���ͼ3�У�ȡBC�е�P��CD�е�Q������PG��GQ��
��AG=GC��CPB��CQ=DQ��
��PG��AB��GQ��QD��
���CPG=��B=60�㣬��CGP=��CAB=60�㣬
���CPG�ǵȱ������Σ�ͬ����֤��CQG�ǵȱ������Σ�
�ɣ�1����֪��CE+CF=PC=$\frac{1}{2}$BC��
�ڽ��ۣ�CE+CF=$\frac{BC}{t}$��
���ɣ���ͼ4�У���GP��AB��BC��P��GQ��AD��CD��Q��
��PG��AB��GQ��QD��
���CPG=��B=60�㣬��CGP=��CAB=60�㣬
���CPG�ǵȱ������Σ�ͬ����֤��CQG�ǵȱ������Σ�
�ɣ�1����֪��CE+CF=PC=CG��
��AC=BC=t•CG��
��CE+CF=$\frac{BC}{t}$��
��3����ͼ4�У���BM��AC��M��
��t��2��
���G���߶�CM�ϣ�
��Rt��ABM�У��ߡ�BMC=90�㣬BM=$\frac{\sqrt{3}}{2}$��8=4$\sqrt{3}$��BG=7��
��MG=$\sqrt{B{G}^{2}-B{M}^{2}}$=$\sqrt{{7}^{2}-��4\sqrt{3}��^{2}}$=1��
��CM=MA=4��
��CG=CM-MG=3��
�ɣ�1����֪��CG=CE+CF��
��CE=CG-CF=3-$\frac{6}{5}$=$\frac{9}{5}$��
���� ����ο��ı����ۺ��⡢ȫ�������ε��ж������ʡ����ε����ʣ��ȱ������ε��ж������ʵ�֪ʶ������Ĺؼ������������Щ֪ʶ������⣬ѧ�����Ӹ����߰�����ת��Ϊ������Ϥ��ͼ�Σ������п��������ͣ�

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д� ��ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ���밴Ҫ���ʴ��������⣺
��ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ���밴Ҫ���ʴ��������⣺ ��ͼ����Բ�η���Ǯ�����й���Ǯ�ҵ�ͻ��������һöԲ�η���Ǯ����뾶Ϊr���м䷽�ױ߳�Ϊa����ͼʾ��Ӱ���ֵ����Ϊr2��-a2��
��ͼ����Բ�η���Ǯ�����й���Ǯ�ҵ�ͻ��������һöԲ�η���Ǯ����뾶Ϊr���м䷽�ױ߳�Ϊa����ͼʾ��Ӱ���ֵ����Ϊr2��-a2��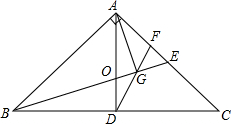 Rt��ABC�У���BAC=90�㣬AB=AC��D��BC�е㣬��FGE=45�㣮
Rt��ABC�У���BAC=90�㣬AB=AC��D��BC�е㣬��FGE=45�㣮