题目内容
16. 如图,小正方形的边长为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据网格中的数据求出AB,AC,BC的长,求出三边之比,利用三边对应成比例的两三角形相似判断即可.
解答 解:根据题意得:AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,BC=2,AC=$\sqrt{{1}^{2}{+3}^{2}}$=$\sqrt{10}$,
∴BC:AC:AB=2:$\sqrt{10}$:$\sqrt{2}$=$\sqrt{2}$:$\sqrt{5}$:1,
A、三边之比为$\sqrt{2}$:$\sqrt{5}$:1,图中的三角形(阴影部分)与△ABC相似;
B、三边之比$\sqrt{2}$:$\sqrt{5}$:3,图中的三角形(阴影部分)与△ABC不相似;
C、三边之比为1:$\sqrt{5}$:2$\sqrt{2}$,图中的三角形(阴影部分)与△ABC相似;
D、三边之比为2:$\sqrt{5}$:$\sqrt{13}$,图中的三角形(阴影部分)与△ABC不相似,
故选A.
点评 此题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解本题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
7.下列运算正确的是( )
| A. | x6÷x3=x2 | B. | (-2x)3=-8x3 | C. | x6•x4=x24 | D. | (x3)3=x6 |
4.下列说法正确的是( )
| A. | -64的立方根是4 | B. | 9的平方根是±3 | ||
| C. | 4的算术平方根是16 | D. | 0.1的立方根是0.001 |
5.在一次汉字听写大赛中,10名学生得分情况如表:
那么这10名学生所得分数的中位数和众数分别是( )
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 85和82.5 | B. | 85.5和85 | C. | 85和85 | D. | 85.5和80 |
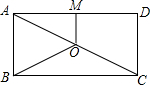 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若OM=3,AD=8,则BO=5.
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若OM=3,AD=8,则BO=5.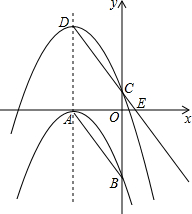 如图,抛物线C1:y=-$\frac{4}{9}$(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,
如图,抛物线C1:y=-$\frac{4}{9}$(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,