题目内容
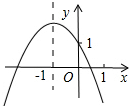 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②b2-4ac>0;③b>0;④4a-2b+c<0;⑤c-a>1,其中正确结论的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②b2-4ac>0;③b>0;④4a-2b+c<0;⑤c-a>1,其中正确结论的是( )| A、①② | B、①③⑤ |
| C、②③⑤ | D、①②⑤ |
考点:二次函数图象与系数的关系
专题:数形结合
分析:利用自变量为1时函数值为负数可对①进行判断;根据抛物线与x轴交点的各数对②进行判断;由抛物线开口方向得到a<0,再由抛物线的对称轴为直线x=-1,得到b=2a<0,于是可对③进行判断;根据抛物线的对称性得到抛物线与x轴的另一个交点在(-2,0)与(-3,0)之间,则x=-2时,函数值为正数,则可对④进行判断;由抛物线与y轴交于(0,1)得到c=1,加上a<0,则可对⑤进行判断.
解答:解:∵x=1时,y<0,
∴a+b+c<0,所以①正确;
∵抛物线与x轴有2个交点,
∴b2-4ac>0,所以②正确;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-
=-1,
∴b=2a<0,所以③错误;
∵抛物线与x轴的一个交点在(0,0)与(1,0)之间,
而抛物线对称轴为直线x=-1,
∴抛物线与x轴的另一个交点在(-2,0)与(-3,0)之间,
∴x=-2时,y>0,
∴4a-2b+c>0,所以④错误;
∵抛物线与y轴交于(0,1),
∴c=1,
而a<0,
∴c-a=1-a>1,所以⑤正确.
故选D.
∴a+b+c<0,所以①正确;
∵抛物线与x轴有2个交点,
∴b2-4ac>0,所以②正确;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=2a<0,所以③错误;
∵抛物线与x轴的一个交点在(0,0)与(1,0)之间,
而抛物线对称轴为直线x=-1,
∴抛物线与x轴的另一个交点在(-2,0)与(-3,0)之间,
∴x=-2时,y>0,
∴4a-2b+c>0,所以④错误;
∵抛物线与y轴交于(0,1),
∴c=1,
而a<0,
∴c-a=1-a>1,所以⑤正确.
故选D.
点评:本题考查了二次函数与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c).当△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
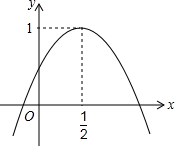 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
下列运算中,正确的是( )
| A、3x+2x2=5x3 |
| B、2a2b-a2b=1 |
| C、-ab-ab=-2ab |
| D、7x+5x=12x2 |

 太原市公共自行车项目是为了缓解交通拥堵、减少环境污染和方便市民出行的民生工程重点项目之一,截止2014年12月,累计租骑公共自行车总量已达到2.217亿车次,这个数据用科学记数法表示为
太原市公共自行车项目是为了缓解交通拥堵、减少环境污染和方便市民出行的民生工程重点项目之一,截止2014年12月,累计租骑公共自行车总量已达到2.217亿车次,这个数据用科学记数法表示为