题目内容
9.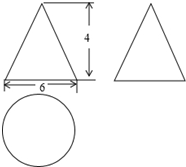 已知一个几何体的三视图如图所示,
已知一个几何体的三视图如图所示,(1)试写出它的形状;
(2)根据已知的数据求出这个几何体的侧面积.
(为了便于说明,可在原图上标上字母和作辅助线)
分析 (1)根据三视图可判断这个几何体为圆锥;
(2)先利用勾股定理计算出母线长,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
解答 解:(1)这个几何体为圆锥;
(2)圆锥的底面圆的半径为3,圆锥的高为4,则圆锥的高=$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以圆锥的侧面积=$\frac{1}{2}$•2π•3•5=15π.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
18.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
则二次函数的解析式为y=-2x2-12x-13.
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |

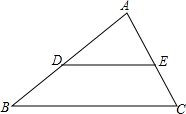 如图,$\frac{BD}{AB}=\frac{CE}{AC}$,BC=20,CE:EA=2:3,求DE的长.
如图,$\frac{BD}{AB}=\frac{CE}{AC}$,BC=20,CE:EA=2:3,求DE的长.