题目内容
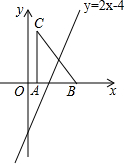 如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-4上时,线段AC扫过的面积为( )
如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-4上时,线段AC扫过的面积为( )A、8
| ||
| B、12 | ||
| C、16 | ||
| D、18 |
考点:一次函数图象上点的坐标特征,坐标与图形变化-平移
专题:计算题
分析:先计算出AB=3,再利用勾股定理计算出AC=4,从而得到C(1,4),由于△ABC沿x轴向右平移,C点的纵坐标不变,则可把y=4代入y=2x-4,解得x=4,于是得到当点C落在直线y=2x-4上时,线段AC向右平移了4-1=3个单位,然后根据矩形的面积公式求解.
解答:解:∵点A、B的坐标分别为(1,0),(4,0),
∴AB=3,
∵∠CAB=90°,BC=5,
∴AC=
=4,
∴C(1,4)
当y=4时,2x-4=4,解得x=4,
∴当点C落在直线y=2x-4上时,线段AC向右平移了4-1=3个单位,
∴线段AC扫过的面积=4×3=12.
故选B.
∴AB=3,
∵∠CAB=90°,BC=5,
∴AC=
| BC2-AB2 |
∴C(1,4)
当y=4时,2x-4=4,解得x=4,
∴当点C落在直线y=2x-4上时,线段AC向右平移了4-1=3个单位,
∴线段AC扫过的面积=4×3=12.
故选B.
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-
,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了平移的性质.
| b |
| k |

练习册系列答案
相关题目
 如图,等边△ABC在平面直角坐标系中的位置如图所示,其中顶点A(-1,-1),B(3,-1),则顶点C的坐标为( )
如图,等边△ABC在平面直角坐标系中的位置如图所示,其中顶点A(-1,-1),B(3,-1),则顶点C的坐标为( )A、(1,2
| ||
B、(0,2
| ||
C、(1,2
| ||
D、(1,2
|
已知在坐标平面内有一点M(3,4),点M关于原点的对称点为N,则点M和点N的距离( )
| A、6 | B、8 | C、10 | D、12 |
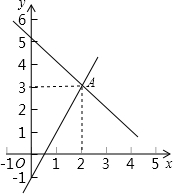 如图,点A的坐标可以看成是方程组
如图,点A的坐标可以看成是方程组