题目内容
16．已知x≠0，且M=（x2+2x+1）（x2-2x+1），N=（x2+x+1）（x2-x+1），试比较M与N的大小．分析 直接利用多项式乘法运算法则求出M-N，进而得出M与N的大小．
解答 解：∵M=（x2+2x+1）（x2-2x+1），N=（x2+x+1）（x2-x+1），
∴M-N=[（x2+2x+1）（x2-2x+1）-（x2+x+1）（x2-x+1）]，
=[（x+1）（x-1）]2-（x2+x+1）（x2-x+1），
=（x2-1）2-（x4-x3+x2+x3-x2+x+x2-x+1）
=x4-2x2+1-（x4+x2+1）
=-2x2，
∵x≠0，
∴x2＞0，
∴-2x2＜0，
∴M-N＜0，
∴M＜N．
点评 此题主要考查了整式的混合运算，正确掌握运算法则是解题关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6．下列每组数分别是三根小木棒的长度（cm），用它们能摆成三角形的是（ ）
| A． | 3 4 9 | B． | 2 3 5 | C． | 5 12 13 | D． | 5 5 11 |
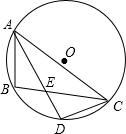如图，AB，AC是⊙O弦，∠BAC的角平分线交⊙O于点D，AD与BC交于点E，若DE=2cm，AE=8cm，则DC=2$\sqrt{5}$cm．